El método aplicado en Tableau para el cálculo de percentiles no es obvio. Para ver cómo funciona, vamos a considerar la siguiente tabla de datos:
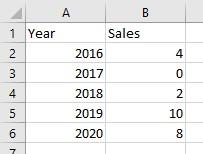
Se trata de 5 valores entre 0 y 10 -escenario muy sencillo-. Si ordenamos los valores (el campo Sales) de menor a mayor, queda el conjunto de valores 0, 2, 4, 8, 10. A partir de ahora, cuando nos refiramos a los valores, estaremos hablando de los valores ordenados.
El procedimiento aplicado comienza por buscar un valor cuya posición en la lista sea equivalente al percentil indicado. Por ejemplo, si indicamos el percentil 0, estaríamos haciendo referencia al primer valor (el valor 0). Si indicamos el percentil 1, estaríamos haciendo referencia al último valor (el valor 10). Si indicamos el percentil 0.5, estaríamos haciendo referencia al valor que ocupe el punto intermedio de la lista. En nuestro ejemplo se trata de 5 valores (número impar), por lo que existe un valor que ocupa el punto intermedio y es 4.
Es muy sencillo, por lo tanto, calcular los percentiles correspondientes a nuestros 5 números:
| Valor | Percentil |
|---|---|
| 0 | 0.00 |
| 2 | 0.25 |
| 4 | 0.50 |
| 8 | 0.75 |
| 10 | 1.00 |
Si tenemos N números, el salto de uno a otro percentil será de 1 / (N - 1).
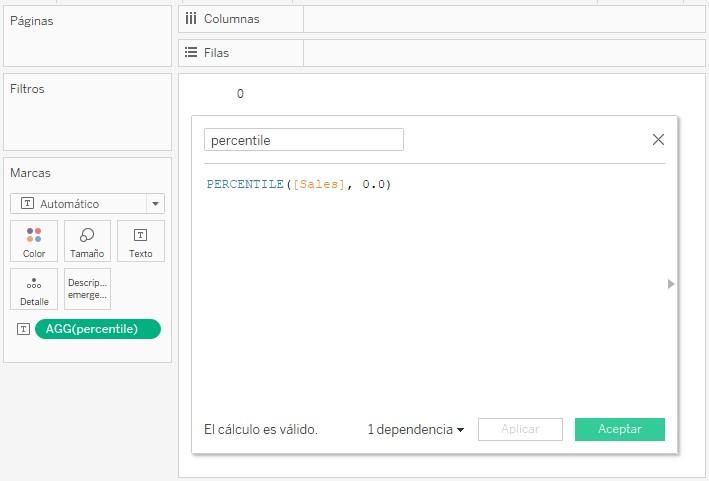
En la siguiente imagen -tras leer la tabla de datos desde Tableau- se ha creado el siguiente campo calculado que devuelve el valor correspondiente al percentil 0:
percentile =
PERCENTILE([Sales], 0.0)
...y se ha llevado al lienzo, obteniéndose el valor 0 como resultado (el primer valor de nuestra lista):
O, si queremos el resultado correspondiente al percentil 0.5:
percentile =
PERCENTILE([Sales], 0.5)
Es decir, se devuelve el valor que ocupa la mitad exacta de la lista (4).
Hasta aquí todo es muy sencillo: si tengo 101 valores (ocupando las posiciones desde la 0 hasta la 100) y quiero el valor equivalente al percentil 0.78, por ejemplo, basta ver qué valor de la lista ocupa la posición 78 una vez hemos ordenado los valores.
La dificultad surge cuando no hay un valor que ocupe la posición en cuestión (por tratarse de una posición no entera). Volvamos a nuestro ejemplo de 5 valores (0, 2, 4, 8, 10).
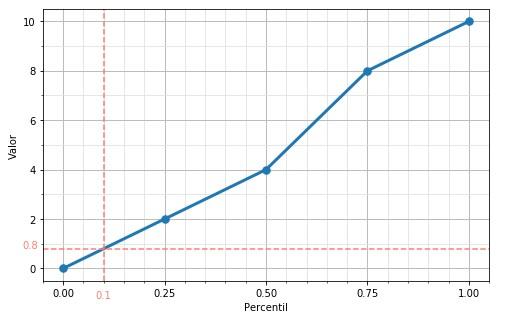
Ahora queremos averiguar el valor correspondiente a, por ejemplo, el percentil 0.1, percentil que no se corresponde con ninguno de los valores que tenemos. El procedimiento entonces es el siguiente: Tableau considera los valores de nuestra lista que tienen los percentiles inmediatamente anterior y posterior (los percentiles 0.0 y 0.25), valores 0 y 2. A continuación realiza una interpolación lineal: Si al percentil 0.0 le corresponde el valor 1 y al percentil 0.25 le corresponde el valor 2, la recta definida por estos valores es
Valor = [(2-0) / (0.25 - 0.0)] * Percentil
Ecuación de la recta que pasa por dos puntos
Según esta recta, el valor correspondiente al percentil 0.1 es (2 * 0.1) / 0.25, es decir, 0.8. Confirmémoslo en Tableau:
percentile =
PERCENTILE([Sales], 0.1)
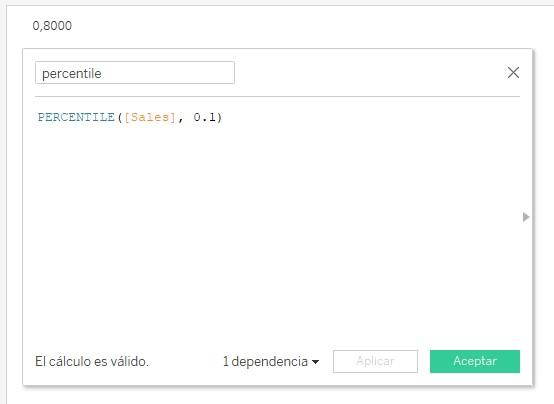
Para otros valores la interpolación a realizar involucrará otros puntos, tal y como se ven en la gráfica mostrada anteriormente. Así, la recta que permite calcular los valores correspondientes a los percentiles en el rango (0.5, 0.75) es
Valor = 16 * Percentil - 4
Hagamos una prueba. Por ejemplo, consideremos el percentil 0.63. Según la recta anterior, el valor asociado sería 16 * 0.63 - 4 = 6.08. Confirmémoslo en Tableu:
percentile =
PERCENTILE([Sales], 0.63)
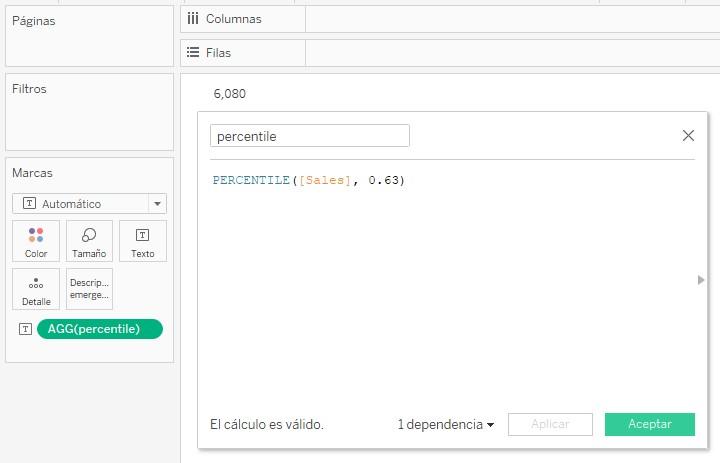
Vemos que la cifra es exactamente la calculada.