Inicio > Recursos educativos > Tutoriales

Implementación de PCA

Aunque solo sea como ejercicio, apliquemos esta técnica para transformar el dataset Iris realizanco los cálculos manualmente. Los pasos a seguir son:

  1. Obtención de la matriz de covarianza de las características
  2. Obtención de los eigenvectors (representando los componentes principales)
  3. Ordenación de éstos según sus eigenvalues
  4. Selección de los N componentes principales correspondientes a las N dimensiones del espacio al que vamos a transformar los datos

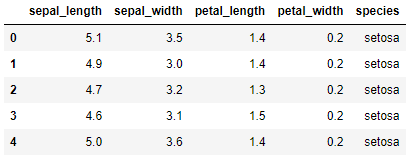
Comenzamos cargando los datos:

data = sns.load_dataset("iris")
data.head()

Implementación de PCA

Y extraemos las características predictivas:

X = data.drop("species", axis = 1)

PCA es muy sensible a la escala de las características, por lo que, si deseamos dar a todas ellas la misma importancia, convendrá escalarlas adecuadamente:

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)

Calculamos ahora la matriz de covarianza de las características predictivas transformadas:

cov_matrix = np.cov(X.T)
cov_matrix
array([[ 1.00671141, -0.11835884,  0.87760447,  0.82343066],
       [-0.11835884,  1.00671141, -0.43131554, -0.36858315],
       [ 0.87760447, -0.43131554,  1.00671141,  0.96932762],
       [ 0.82343066, -0.36858315,  0.96932762,  1.00671141]])

Podemos obtener los eigenvectors (vectores propios) y eigenvalues (valores propios) de la matriz de covarianza usando la función np.linelg.eig() de NumPy:

eig_values, eig_vectors = np.linalg.eig(cov_matrix)

Los vectores propios (vectores que, en general, al ser transformados solo van a ver modificado su módulo, no su dirección) son los siguientes:

eig_vectors
array([[ 0.52106591, -0.37741762, -0.71956635,  0.26128628],
       [-0.26934744, -0.92329566,  0.24438178, -0.12350962],
       [ 0.5804131 , -0.02449161,  0.14212637, -0.80144925],
       [ 0.56485654, -0.06694199,  0.63427274,  0.52359713]])

Los vectores propios están situados en columnas. Ésta es la matriz que va a transformar los datos desde el espacio original hasta el nuevo espacio.

Los eigenvalues (escalares por los que se multiplicarán los vectores propios cuando sean transformados y que representan la varianza explicada por el componente principal correspondiente) son los siguientes:

eig_values
array([2.93808505, 0.9201649 , 0.14774182, 0.02085386])

Estos valores nos permiten estimar el porcentaje de varianza de las características originales explicada por cada componente principal, simplemente dividiendo cada valor por la suma de los cuatro valores:

eig_values / eig_values.sum()
array([0.72962445, 0.22850762, 0.03668922, 0.00517871])

Vemos que, en el dataset Iris, el primer componente principal supone el 72.9% de la varianza total.

Ordenamos los vectores propios según sus valores propios, en orden decreciente:

idx = eig_values.argsort()[::-1]
eig_values = eig_values[idx]
eig_vectors = eig_vectors[:, idx]
eig_vectors
array([[ 0.52106591, -0.37741762, -0.71956635,  0.26128628],
       [-0.26934744, -0.92329566,  0.24438178, -0.12350962],
       [ 0.5804131 , -0.02449161,  0.14212637, -0.80144925],
       [ 0.56485654, -0.06694199,  0.63427274,  0.52359713]])

(en nuestro caso la matriz no ha cambiado)

Y, ahora, podríamos seleccionar solo los dos primeros componentes principales, reduciendo, de esta forma, nuestro dataset a dos características:

W = eig_vectors[:, :2]
X_pca = X.dot(W)
X_pca[:5]
array([[-2.26470281, -0.4800266 ],
       [-2.08096115,  0.67413356],
       [-2.36422905,  0.34190802],
       [-2.29938422,  0.59739451],
       [-2.38984217, -0.64683538]])

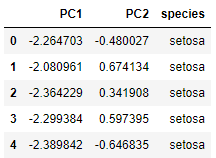
Reconstruyamos el DataFrame con estas características:

data_pca = pd.DataFrame(X_pca, columns = ['PC1', 'PC2'])
data_pca = pd.concat([data_pca, data['species']], axis = 1)
data_pca.head()

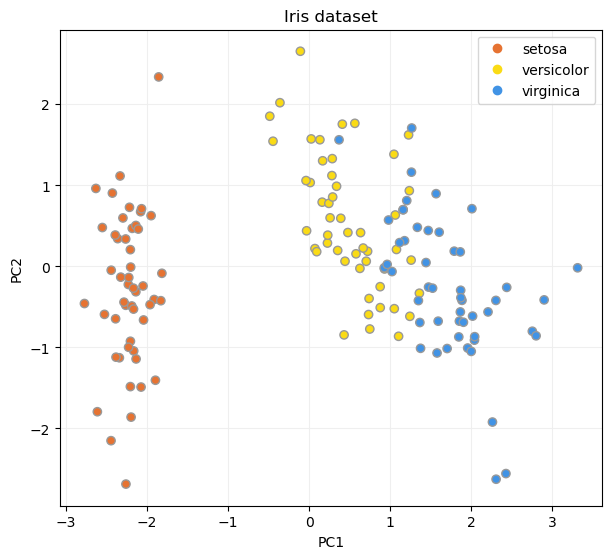
Implementación de PCA

Y mostremos el resultado en un diagrama de dispersión:

fig, ax = plt.subplots(figsize = (7, 7))
ax.set_aspect("equal")
scatter = ax.scatter(
    x = data_pca.PC1, y = data_pca.PC2,
    c = data_pca.species.astype("category").cat.codes,
    zorder = 2, edgecolor = "#999999",
    cmap = ListedColormap(["#E67332", "#FADB15", "#4193E5"])
)
ax.set_title("Iris dataset")
ax.set_xlabel("PC1")
ax.set_ylabel("PC2")
ax.legend(
    handles = scatter.legend_elements()[0],
    labels = list(data_pca.species.unique())
)
ax.grid(color = "#EEEEEE", zorder = 1, alpha = 0.9)
plt.show()
Implementación de PCA