Para ver con un ejemplo sencillo a qué nos estamos refiriendo, considérese el siguiente conjunto de datos:
df = pd.DataFrame({
"x": [2, 4, 8, 12],
"y": [1, 2, 4, 6]
})
df

Se trata de un conjunto de datos de dos dimensiones (dos características). Si lo mostramos en una gráfica obtenemos lo siguiente:
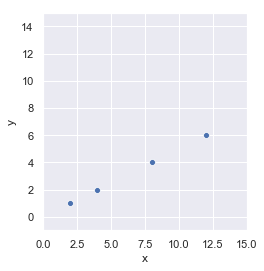
Es inmediato apreciar (si no lo habíamos hecho ya al ver la tabla de datos) que los puntos se encuentran sobre una misma recta:
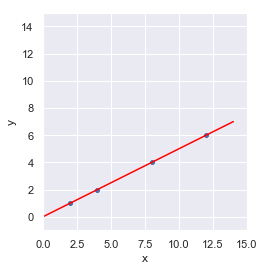
...lo que nos lleva a deducir que, para comunicar la posición de los puntos, no era necesario dar las coordenadas x e y de cada uno de ellos. Hubiese bastado indicar la posición de cada punto sobre dicha recta (es decir, una única dimensión). Un resultado análogo sería el girar la recta anterior de forma que quedase situada sobre el eje x:
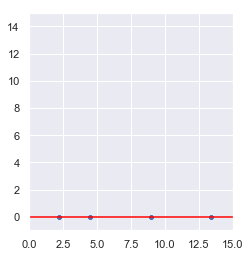
Para ello tendríamos que transformar los puntos originales de forma que su nueva posición x fuese la distancia del punto original al centro de coordenadas (la distancia euclídea: la raiz cuadrada de la suma de los cuadrados de x y de y). Ahora los puntos vendrían dados por:
d = (df.x ** 2 + df.y ** 2) ** (1/2)
df_transformado = pd.DataFrame({"x" : round(d, 4), "y": [0.0] * 4})
df_transformado
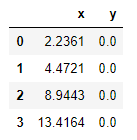
Nuevamente, podríamos obviar la característica y, que tras la transformación no aporta información, y trabajar en un espacio de una única coordenada.
Esto, por supuesto, tiene sentido si la transformación realizada no supone pérdida de información necesaria para el análisis que se esté realizando. Si estamos interpolando puntos, la transformación realizada no supone pérdida alguna: podríamos seguir interpolando puntos trabajando con una única característica y convertir el resultado al espacio original de dos características. En otros escenarios, tal vez no sea posible.