La regresión softmax (o Multinomial Logistic Regression) es una generalización de la regresión logística que permite aplicarla en escenarios multiclase. A la hora de predecir la clase de una muestra, el modelo calcula un score para cada clase y hace pasar el vector de scores por la función softmax (también llamada exponencial normalizada). Esta función viene definida por la siguiente fórmula:
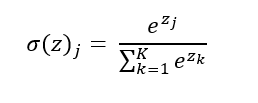
Básicamente, lo que hace es convertir un vector z de k números reales en otro vector de k números en el rango [0, 1] de tal forma que estos k números sumen 1. Podríamos decir que estima la distribución de probabilidad de los k números reales iniciales, lo que consigue calculando la exponencial de cada valor y dividiéndola por la suma de las exponenciales de todos los valores (para normalizarlos y devolver un conjunto de números que sumen 1).
Esta función puede ser implementada en Python de la siguiente forma:
def softmax(x):
return np.exp(x) / np.sum(np.exp(x), axis = 0)
Probémosla con un vector arbitrario de números reales:
v = [2, -1, 4]
softmax(v)
array([0.11849965, 0.00589975, 0.8756006 ])
Podemos confirmar que los valores resultantes suman 1:
sum(softmax(v))
1.0
Este proceso es el seguido por la regresión softmax: estima las probabilidades de cada clase y devuelve la clase correspondiente a la máxima probabilidad estimada.
La función de coste utilizada es la llamada cross entropy:
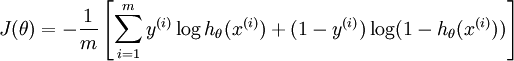
...que es equivalente a la función de coste de la regresión logística cuando solo hay dos clases.
La clase sklearn.linear_model.LogisticRegression de Scikit-learn utiliza una estrategia de uno-versus-todos por defecto si hay más de dos clases implicadas, pero fijando el argumento multi_class a "multinomial" forzamos que se utilice la regresión softmax.