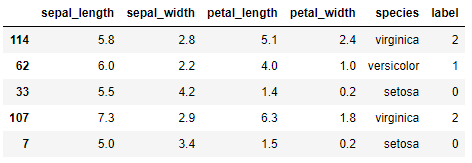
Para ver con un poco de detalle cómo funciona la clase ShuffleSplit, realicemos un ejemplo apenas con 5 muestras de Iris:
iris_copy
Creamos los datasets de entrenamiento y validación:
y_copy = iris_copy.label
Importamos la clase ShuffleSplit y la instanciamos:
Se han especificado 5 divisiones de los datos, y, en cada una, se considerarán 2 muestras en el conjunto de validación (y el resto en el conjunto de entrenamiento: 3 muestras).
Ahora, el método .split() va a ir generando los índices de las muestras que caen en los conjuntos de entrenamiento y de pruebas. Podemos usar un bucle para generar los índices en todas las divisiones y mostrarlos en pantalla:
print(train_index, test_index)
[1 4 3] [0 2]
[4 0 2] [1 3]
[2 4 0] [3 1]
[3 1 0] [4 2]
Comprobamos que hay muestras que son consideradas en el bloque de validación un número diferente de veces (la muestra 2 aparece 3 veces, mientras que la muestra 4 solo aparece una vez, por ejemplo), pudiendo darse el caso de que, tal y como se ha comentado, haya muestras que no se consideren nunca.
Probemos esta clase en el dataset original entrenando los modelos. Reinstanciamos la clase especificando 10 divisiones y que el 25% de las muestras se agrupen en el bloque de validación (también podríamos especificar un número concreto de ellas como hemos hecho en el ejemplo anterior):
Y realizamos la división entrenando los modelos. Los porcentajes de acierto los almacenamos en la lista scores:
for train_index, test_index in ss.split(X):
model.fit(X.iloc[train_index], y.iloc[train_index])
scores.append(model.score(X.iloc[test_index], y.iloc[test_index]))
Echemos un vistazo a éstos:
0.9210526315789473,
0.9473684210526315,
0.9473684210526315,
0.9736842105263158]
Para calcular el valor medio podemos convertir la lista en un array NumPy y aplicar el método .mean():