El método de Principal Component Analysis (PCA, o Análisis de Componentes Principales) gira los datos de forma que, desde un punto de vista estadístico, no exista una correlación entre las características rotadas pero que conserven la mayor cantidad posible de la varianza de los datos originales. Tras realizar la transformación suele realizarse una selección de las nuevas características.
Explicado de forma simple, PCA reduce la dimensionalidad de un conjunto de datos proyectándolos sobre un subespacio de menor dimensionalidad. Por ejemplo, datos con dos características (dispuestos en un plano) pueden ser proyectados sobre una línea tal y como vimos en el ejemplo de la introducción. O un conjunto de datos de tres características (dispuestos en un espacio de tres dimensiones) pueden ser proyectados en un plano (de dos dimensiones). En incluso aquí, los datos resultantes en el plano podrían ser reducidos a una única línea, pasando de las tres dimensiones originales a una sola.
En general, un conjunto de datos de n dimensiones puede ser reducido "proyectándolo" sobre un subespacio de m dimensiones, siendo m menor que n. Por ejemplo, consideremos el siguiente conjunto de muestras pertenecientes a un conjunto de datos de dos dimensiones:
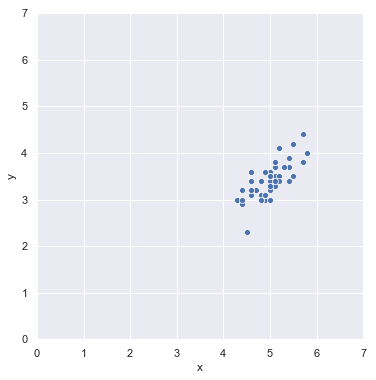
Las muestras forman una cierta elipse, por lo que podría plantearse proyectar los puntos sobre una recta que, probablemente, se aproximaría al eje mayor de aquella. Como esta línea es sobre la que más varían los datos mostrados, sería la asociada al primer componente principal. El segundo componente principal debe ser ortogonal al primero (de hecho debe ser ortogonal a todos los componentes principales), por lo que, en el caso del plano, estaría asociado a la recta perpendicular.
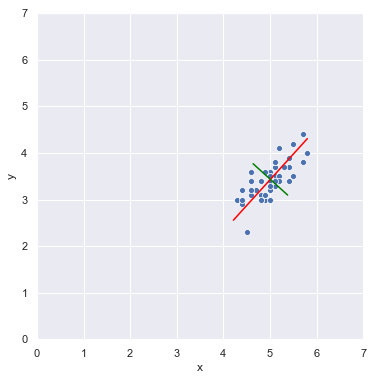
En la imagen anterior se muestra en rojo la recta correspondiente al primer componente principal, recta sobre la que se proyectarían los puntos en el caso de querer reducir la dimensionalidad del conjunto de datos. En verde, perpendicular a la anterior, se muestra la recta asociada al segundo componente principal.
Estos datos tienen la máxima variación a lo largo de la recta correspondiente al primer componente principal, por lo que proyectarlos sobre dicha recta supone mantener la varianza a lo largo de dicho eje aun cuando se esté perdiendo la información de la varianza correspondiente al eje perpendicular (definido por la línea verde). En todo caso, con esta proyección se estaría reduciendo la dimensionalidad manteniendo la mayor información posible sobre la varianza del conjunto de datos original.