Una vez entendido que el error SSE se distribuye en forma de óvalos alrededor del punto para el que el error SSE es cero, supongamos que introducimos una penalización aplicando la regularización L2. Es decir, una penalización mayor cuanto mayor es la distancia que separa al punto del centro de coordenadas. Esto supondría que el punto para el que el error SSE es cero puede que ya no sea el punto para el que el error total sea menor debido a la penalización. Ahora, ese punto para el que el error total sea 0 se habrá desplazado hacia el centro de coordenadas, lo que supondrá una simplificación del modelo (que era el objetivo perseguido).
Si mostramos el error SSE y la penalización, el esquema sería el siguiente:
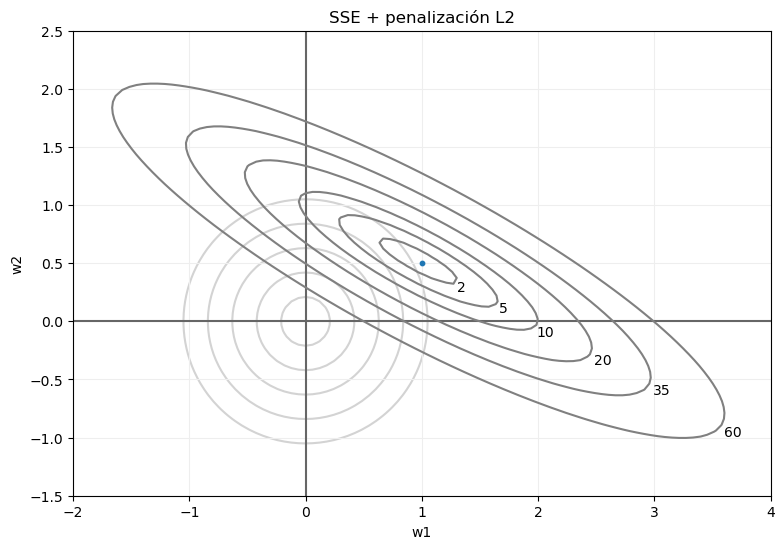
Los puntos que formaban la curva de nivel SSE = 35 (por ejemplo), tras añadir la penalización no van a devolver el valor 35 como resultado de la función de error total, sino que este error será mayor cuanto más alejados estén del centro. O, dicho con otras palabras, de toda esa curva de nivel, el punto que devuelva el menor error va a ser el más próximo al centro de coordenadas (en rojo en la siguiente imagen):
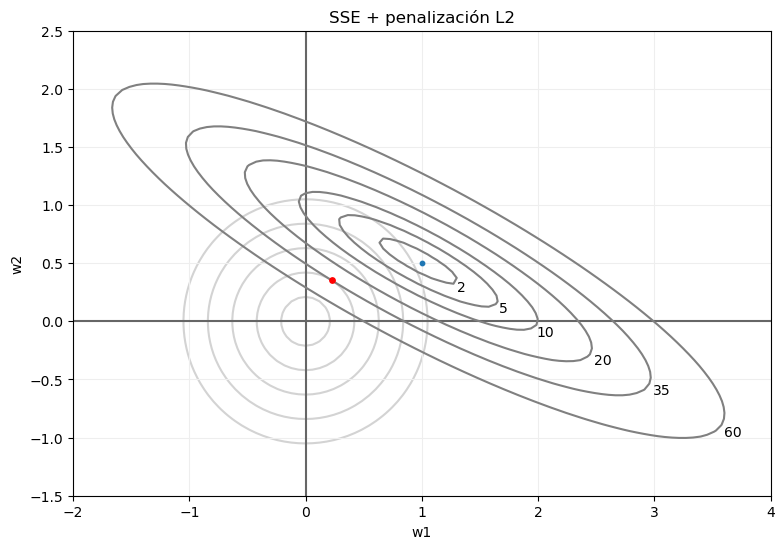
La posición exacta del punto que devuelva el menor error total dependerá, en general, de los datos y del coeficiente de regularización, pero parece lógico esperar que ese punto vaya a ser el más próximo al centro de coordenadas para alguna curva de nivel representando el error SSE, y ese punto, en general, no va a quedar encima de los ejes de coordenadas.