Para entender el proceso, partimos de la base de que tenemos solo dos características predictivas, w1 y w2 (lo que nos va a permitir llevar al plano el error cometido) y, por concretar, supongamos que los datos que queremos aproximar con un modelo son los siguientes:
x = np.linspace(0, 1, 100)
y = x + np.random.normal(loc = 0, scale = 0.1, size = 100) + 0.5
data = pd.DataFrame({'x': x, 'y': y})
Como vemos, se trata de puntos aleatorios alrededor de una recta de pendiente 1 y corte con el eje de ordenadas en el punto 0.5. Podemos visualizarlos para tener una mejor idea de su distribución:
ax.scatter(x = data.x, y = data.y, zorder = 10)
ax.set_xlim(0)
ax.set_ylim(0)
ax.grid(color = "#EEEEEE", zorder = 0)
ax.set_xlabel("x")
ax.set_ylabel("y")
plt.show()
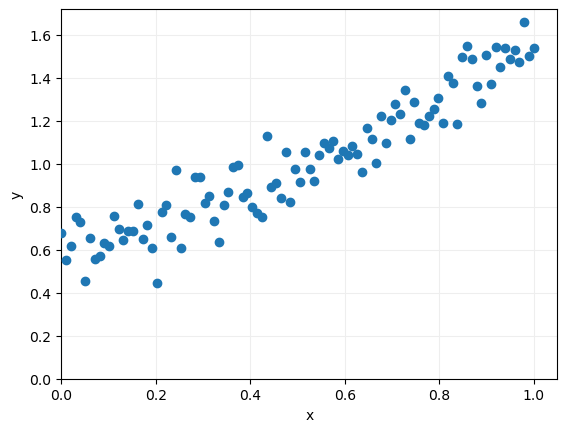
El objetivo es aproximar estos datos con una recta de regresión de la forma
Donde w1 definirá la pendiente y w2 el corte con el eje de ordenadas. Lógicamente, para cada par de coeficientes (w1, w2) cometeremos un error que vamos a suponer que mediremos usando la suma de los cuadrados de los errores individuales (SSE = Sum of Squared Error). Es decir, dada una pareja de coeficientes (w1, w2), el error total se calculará comparando, para cada punto de nuestro dataset, la predicción de nuestra recta de regresión ŷ con el valor real y, elevando al cuadrado la diferencia y sumando todos los errores parciales.
Podemos escribir la función que calcula este coste en función de los datos y los coeficientes w1 y w2 con el siguiente código:
y_pred = w1 * data.iloc[:, 0] + w2
return np.sum(np.square(data.iloc[:, 1] - y_pred))