Tal y como se ha comentado, los vectores correspondientes al bloque de entrenamiento son mapeados a un espacio de mayor dimensionalidad por una cierta función, y este mapeo es responsabilidad de lo que denominamos kernel. Un kernel viene determinado por una matriz cuadrada de dimensión igual al número de muestras siendo analizadas, y el contenido de esta matriz es la resultante de aplicar la función de mapeo al conjunto de entrenamiento.
Scikit-learn ofrece 4 kernels básicos. En las siguientes fórmulas xi y xj representan los valores de la matriz de coeficientes del conjunto de entrenamiento, XT la transpuesta de X, ‖X‖ representa la norma L2 de X, y el punto (.) representa el producto de dos matrices.
Linear
La función aplicada es:
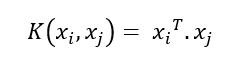
Polynomial
En el kernel polinómico la función aplicada es:
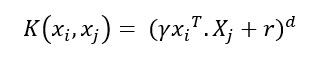
...donde γ viene dada por el parámetro gamma de la función SVC, r por coef0 y d por el parámetro degree.
Radial Basis Function
La función aplicada es:
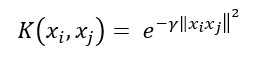
‖Xi-Xj‖ representa una matriz cuadrada con la distancia euclídea entre cada par de puntos de X. Esta matriz puede conseguirse con la función sklearn.metrics.pairwise.euclidean_distances. Al igual que en el caso del kernel polinómico, γ viene dado por el parámetro gamma de SVC.
Sigmoid
En este último caso la función aplicada es:
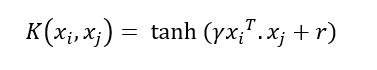
...donde γ y r vienen dados por los parámetros gamma y coef0, respectivamente.