Pues bien, la llamada "ecuación normal" nos devuelve los valores del vector W que minimizan esta ecuación:
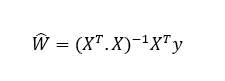
Probemos esta ecuación: Generamos 100 puntos aleatorios en torno a la recta 4 + 3x:
X = 10 * np.random.rand(100, 1)
y = 4 + 3* X + np.random.randn(100, 1)
sns.scatterplot(x = X.reshape(-1, ), y = y.reshape(-1, ));
sns.lineplot(x = [0, 10], y = [4, 34], color = "red");
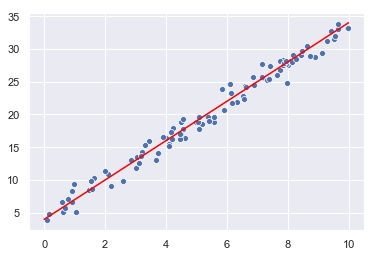
Necesitamos añadir el valor 1 (término independiente) a cada una de las muestras X generadas. En este momento la estructura X tiene esta forma:
X[:5]
array([[1.639099 ],
[3.65892145],
[7.43340226],
[4.24505479],
[8.06951288]])
Añadimos el 1:
X_1 = np.c_[np.ones((100, 1)), X]
Ahora X tiene esta forma:
X_1[:5]
array([[1. , 3.64658257],
[1. , 3.44137047],
[1. , 7.16354034],
[1. , 8.00967176],
[1. , 2.26447014]])
Calculamos la ecuación normal para las estructuras X e y:
best_W = np.linalg.inv(X_1.T.dot(X_1)).dot(X_1.T).dot(y)
best_W
array([[4.26075573],
[2.93751853]])
La recta que minimiza la suma de mínimos cuadrados es (redondeando los coeficientes) 4.26 + 2.93x, lo que está muy cerca de la ideal 4 + 3x (si no hubiésemos añadido el ruido gaussiano).
Una vez obtenidos los parámetros que definen la recta, para realizar una predicción en un punto basta con calcular el valor de la recta en dicho punto.
Es necesario destacar que la resolución de la ecuación normal resulta muy lenta cuando el número de características es elevado (por ejemplo, 100.000 características).
En el lado positivo, una vez ha sido entrenado, las predicciones resultan extremadamente rápidas.