Ahora podríamos plantearnos visualizar el error cometido con nuestros datos para diferentes parejas de parámetros (w1, w2). Por ejemplo, creemos una malla de 100 x 100 puntos barriendo el rango (-2, 4) para el primer parámetro y el rango (-2, 3) para el segundo (recordemos que los valores de los que partieron los datos eran (1, 0.5):
y = np.linspace(-2, 3, 100)
X, Y = np.meshgrid(x, y)
Llevamos las coordenadas de dos en dos a un array NumPy, calculamos el error cometido para cada pareja y redimensionamos el resultado para volver a darle el tamaño 100 x 100 original:
Z = np.array([sse(data, w1, w2) for w1, w2 in p]).reshape(X.shape)
Z contiene ahora un array de 100 x 100 puntos en los rangos comentados, conteniendo el error SSE cometido en cada uno de esos puntos (que recordemos que representan parejas de parámetros (w1, w2)).
El punto para el que el error es mínimo puede obtenerse con la función np.polyfit():
sse_0
punto próximo al (1, 0.5) usado para generar los datos.
Ahora, si llevamos los errores almacenados en Z a una gráfica mostrando, por ejemplo, aquellos puntos que representan los errores 2, 5, 10, 20, 35 y 60 (y los mostramos como curvas de nivel), el resultado es el siguiente:
ax.set_aspect("equal")
ax.contour(X, Y, Z, levels = [2, 5, 10, 20, 35, 60], colors = "gray", zorder = 10)
ax.set_xlim(-2, 4)
ax.set_ylim(-1.5, 2.5)
ax.axhline(0, color = "#666666")
ax.axvline(0, color = "#666666")
ax.grid(color = "#EEEEEE", zorder = 0)
ax.set_xlabel("w1")
ax.set_ylabel("w2")
ax.scatter(1, 0.5, zorder = 10, s = 10)
ax.set_title("SSE")
ax.text(1.30, 0.26, "2")
ax.text(1.66, 0.08, "5")
ax.text(1.99, -0.13, "10")
ax.text(2.48, -0.37, "20")
ax.text(2.99, -0.63, "35")
ax.text(3.6, -0.99, "60")
plt.show()
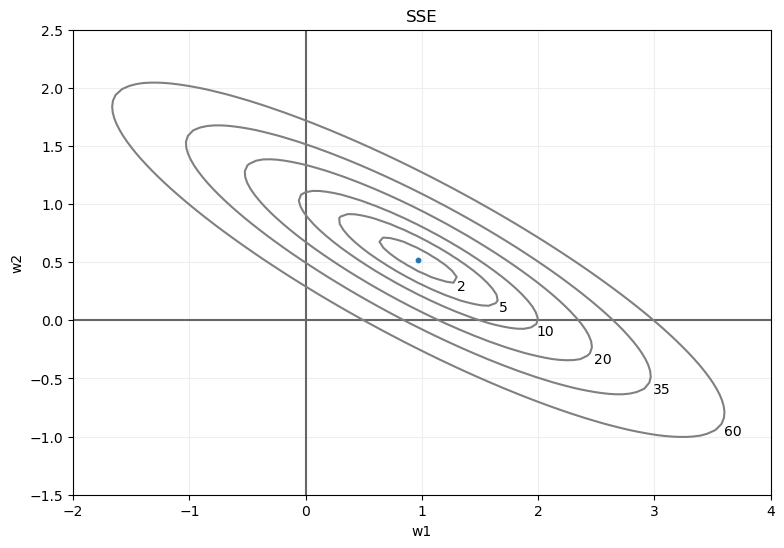
Comprobamos que las curvas de nivel tienen aspecto de óvalos. Si nos fijamos, por ejemplo, en la curva correspondiente a SSE = 35 (quinta desde el interior), representa aquellas combinaciones de parámetros (w1, w2) para los que el error cometido es el mismo e igual a 35.
En las coordenadas (sse_0[0], sse_0[1]) se muestra el punto para el que el error es el menos posible (y supongamos que éste es cero).