Sin embargo, esto cambia radicalmente si la regularización aplicada es la L1, pues ahora la penalización asociada a cada punto no depende de la distancia al centro de coordenadas, sino a la suma de los valores absolutos de sus coordenadas. El esquema ahora sería el siguiente:
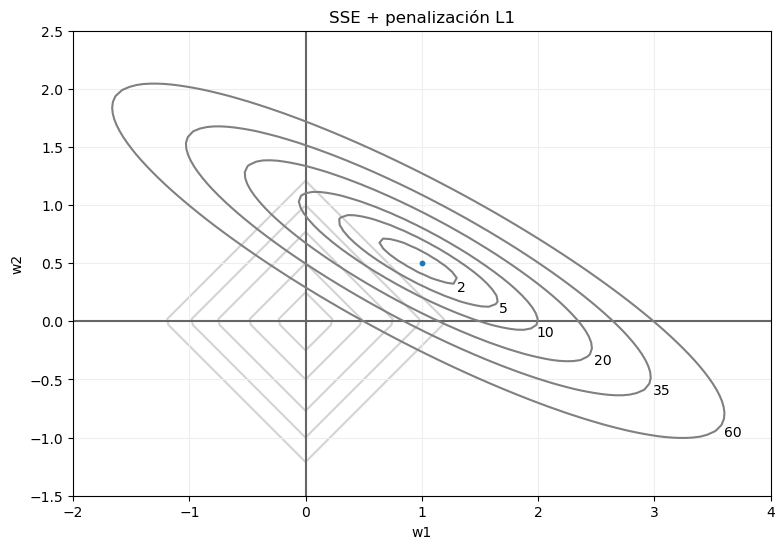
Si volvemos a fijarnos en, por ejemplo, los puntos para los que el error SSE tomaba el valor 35, tras la penalización no van a devolver ese valor. Por el contrario, el error total dependerá de los valores absolutos de sus coordenadas. O, dicho con otras palabras, el punto de dicha curva de nivel para el que el error total sea mínimo será aquel para el que la suma de los valores absolutos de sus coordenadas sea mínimo, lo que, en el ejemplo que estamos viendo, sería el marcado en rojo en la siguiente imagen:
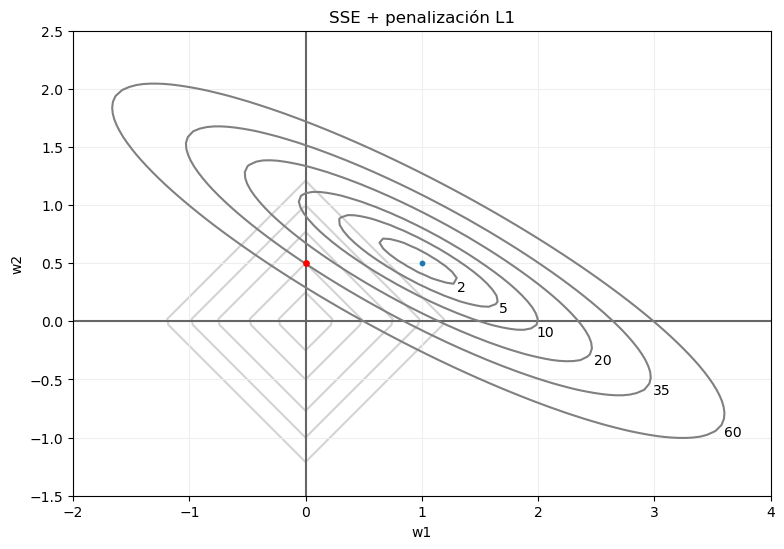
También en este caso, la posición exacta del punto para el que el error total sea mínimo dependerá de los datos y del coeficiente de regularización. Pero resulta comprensible esperar que este punto se encuentre sobre alguno de los ejes de coordenadas. Esto significa que, en el caso que estamos planteándonos con solo dos parámetros, hemos pasado de un vector de parámetros (w1, w2) para el que el error SSE es el mínimo posible, pero implicando una excesiva complejidad del modelo, a otro vector de parámetros (0, w2') para el que el error SSE no es el mínimo posible, pero es óptimo desde el punto de vista del error total (SSE + penalización), e implicando una menor complejidad del modelo.
En un caso general de n parámetros, estaríamos pasando de un vector de parámetros
a otro del tipo (por ejemplo)
en el que un cierto número de los parámetros toma el valor 0, parámetros para los que las características predictivas asociadas resultarían -desde este punto de vista- irrelevantes, reduciéndose, de esta forma, la dimensionalidad del dataset con el que estemos trabajando.