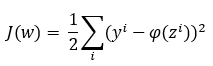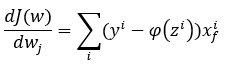Hasta ahora hemos estado dando por sentado que es posible obtener el gradiente de la función de error para una combinación dada de los parámetros del modelo.
En el caso de la Adaline:
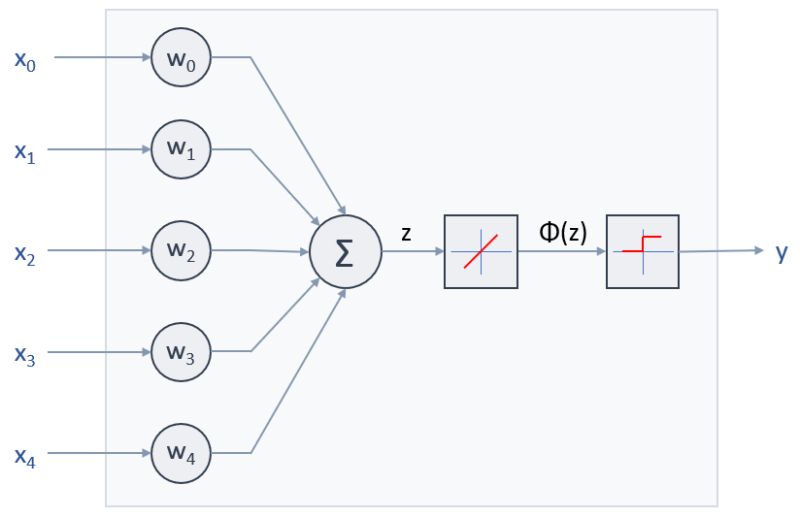
ya se comentó que se suele asumir que la función de error involucrada es la siguiente:
Si tenemos en cuenta que ϕ(z) no es más que la combinación lineal de los valores de entrada ponderados, resulta muy sencillo obtener la derivada parcial de la función con respecto a cualquiera de los parámetros wi. Concretamente:
Pero, en una red neuronal en la que los valores de entrada de unas neuronas son las salidas de otras neuronas, la formulación de la función de error puede complicarse enormemente. En realidad, basta con intentar formular la función de error de una red neuronal con unas pocas neuronas para entender la complejidad de la tarea. No digamos nada, por lo tanto, de una red neuronal formada por millones, o por centenares de miles de millones de neuronas.
Y si la formulación de la función de error ya de por sí es compleja, imaginemos derivar la función con respecto a todos y cada uno de sus parámetros (pesos y bias). Es físicamente imposible. En estas condiciones se recurre a enfoques matemáticas que permiten obtener estas derivadas en cadena, comenzando por las últimas neuronas y recorriendo la red neuronal hacia la entrada. Este método, conocido como backpropagation, será comentado más adelante.