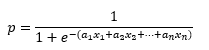Es decir, al igual que ocurre con el Perceptrón y la Adaline, la regresión logística también calcula una suma ponderada de las características predictivas, pero en lugar de devolver dicho resultado, lo pasa por la función sigmoide para devolver un valor en el rango (0, 1) que se interpreta como una probabilidad. A la hora de entrenar el modelo para obtener los parámetros (pesos y bias) que minimizan la función de coste, el objetivo es asignar altas probabilidades a las muestras positivas (aquellas para las que la variable objetivo toma el valor 1) y bajas probabilidades para las muestras negativas, lo que se consigue con la siguiente función de coste para una única instancia:
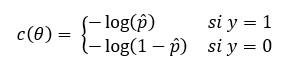
siendo p̂ la probabilidad asignada a una muestra.
Se muestran a continuación ambas gráficas:
x = np.linspace(0.0000001, 0.9999999, 100)
fig, ax = plt.subplots(1, 2, figsize = (10, 5))
y = -np.log(x)
sns.lineplot(x = x, y = y, color = "DodgerBlue", ax = ax[0]);
ax[0].set_xlim(0, 1)
ax[0].set_ylim(0, 10)
ax[0].set_title("-log(p)")
y = -np.log(1 - x)
sns.lineplot(x = x, y = y, color = "DodgerBlue", ax = ax[1]);
ax[1].set_xlim(0, 1)
ax[1].set_ylim(0, 10)
ax[1].set_title("-log(1-p)");
plt.show()
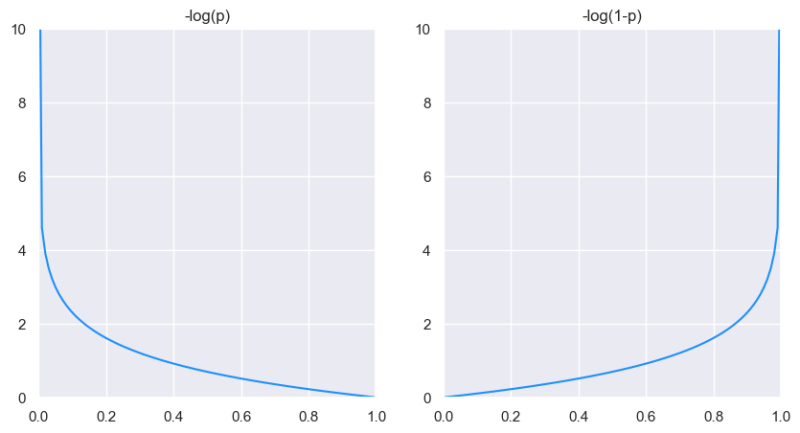
Si a una muestra positiva (aquella con una etiqueta asignada igual a 1) se le asigna una probabilidad próxima a 0, el coste tiende a infinito (y, al revés, si se le asigna una probabilidad próxima a 1, el coste tenderá a 0). Por el contrario, si se trata de una muestra negativa (aquella con una etiqueta asignada igual a 0), el asignarle una probabilidad próxima a 1 supondría un coste también tendiente a infinito y asignarle una probabilidad próxima a 0 supondría un coste próximo a 0.
La función de error correspondiente al dataset completo es simplemente el valor medio de la suma del error de todas las muestras, es decir:
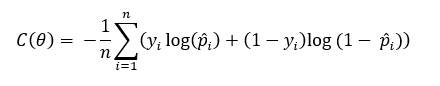
Esta función se conoce como log loss o cross-entropy (entropía cruzada), y al ser convexa y derivable, nos permite aplicar optimizadores como Gradient Descent para obtener su valor mínimo, para lo que habría que calcular las derivadas parciales de la función con respecto a los parámetros del modelo, y recordemos que la probabilidad asignada a cada muestra depende de éstos a través de la función sigmoide: