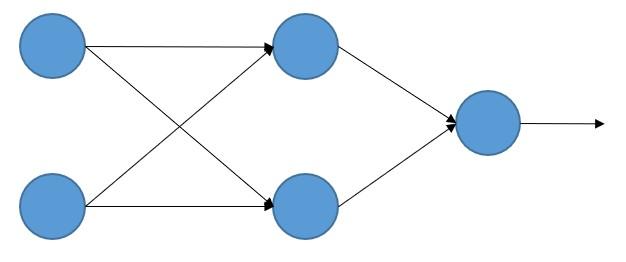
Antes de seguir, parémonos un momento a entender cómo el error cometido por la red neuronal depende de los pesos y bias de las neuronas. Supongamos que estamos trabajando en un entorno de regresión (en el que queremos obtener no la clasificación de cada muestra de entrada, sino un valor numérico asociado a ellas), y que estamos usando una sencilla red neuronal (un perceptrón multicapa) que recibe dos valores de entrada, con una capa oculta que contiene dos neuronas y, lógicamente -al tratarse de un análisis de regresión-, una única neurona de salida:
Esta arquitectura es la que hemos usado en una sección previa. Si mostramos los parámetros involucrados en la red (pesos y bias) el resultado es también conocido:
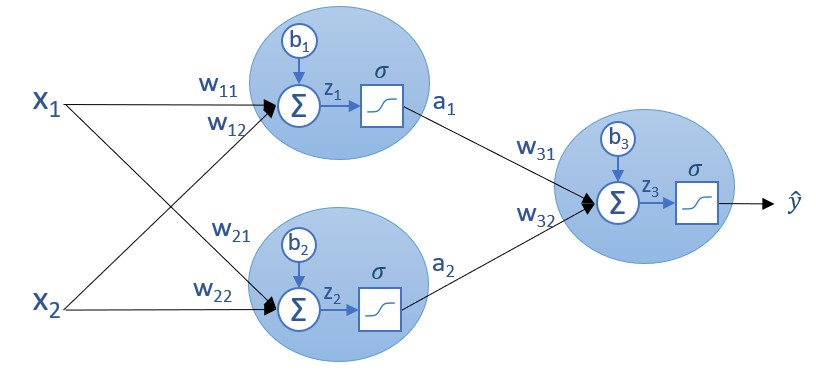
Supongamos que inicialmente los parámetros (pesos y bias) toman unos ciertos valores, los que sean. E imaginemos ahora que nuestros datos de entrenamiento son los siguientes (no es más que un ejemplo):
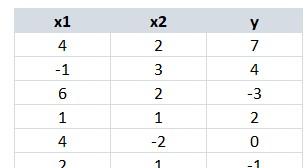
En la imagen anterior vemos dos columnas con las características predictivas, x1 y x2, y una columna con la etiqueta o valor objetivo, y.
Si quisiéramos saber cuál es el error cometido por nuestra red -con la configuración que tenga- para este conjunto de entrenamiento, tendríamos que ir pasando las características predictivas (x1 y x2) por la red, ver cuál es el resultado o salida para cada valor, ŷi, y comparar este valor con el valor objetivo, yi.
Para una muestra concreta i podríamos calcular el error como el cuadrado de la diferencia (u otro criterio que nos conviniese) de estos valores:
Ci = (ŷi - yi)2
Para todo el dataset, el error total cometido podríamos calcularlo simplemente como la suma de los errores individuales:
C = ?(ŷi - yi)2
El objetivo del entrenamiento sería configurar la red (escoger los valores de los pesos y bias) de forma que se minimizase el error total cometido.