Como podemos ver, en este ejemplo idealizado el píxel situado en las coordenadas (0, 4) -fila 0 y columna 4- está activo en los 4 dígitos, por lo que no aporta información útil:
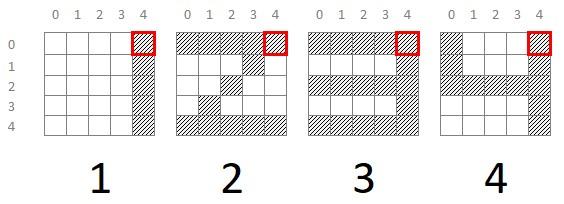
Sin embargo, el píxel (2, 0) nos permite separar nuestros dígitos en dos bloques: uno -con el píxel desactivado- formado por los dígitos 1 y 2, y otro -con el píxel activo- formado por los dígitos 3 y 4:
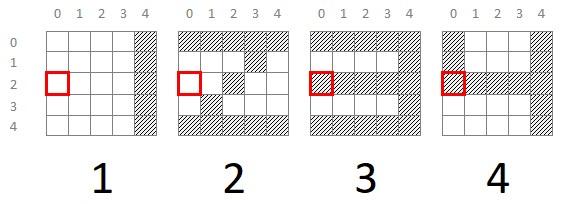
Una vez identificado este píxel que nos permite separar los dígitos en dos grupos, podríamos analizar cada uno de los grupos y buscar otros píxels que, a su vez, nos permitieran seguir identificando otros subgrupos. Así, si analizamos el grupo formado por los dígitos 3 y 4, podemos ver fácilmente que el píxel (0, 2), por ejemplo, nos permite clasificar las muestras correspondientes a ambos dígitos: el número 3 si este píxel está activo y el número 4 si no lo está:
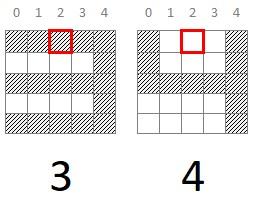
Es decir, los píxels (2, 0) y (0, 2) nos permitirían clasificar de forma unívoca estos dos dígitos (para el dataset idealizado con el que estamos jugando).
Por supuesto, los dígitos manuscritos presentan una cierta variación con respecto a su representación "ideal", pero desde un punto de vista estadístico siguen existiendo patrones que son fácilmente identificables por, por ejemplo, un árbol de decisión.