También es encarable este dataset por algoritmos de tipo "k-vecinos". Por ejemplo, supongamos dos imágenes representando dos versiones distintas del número 3:
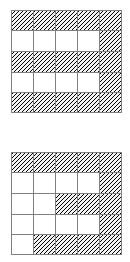
Si superponemos ambas imágenes, podemos comprobar que muchos píxels son comunes. Otra forma de verlo es "aplanar" ambos grids (mostrando los píxels de cada fila en una única fila):
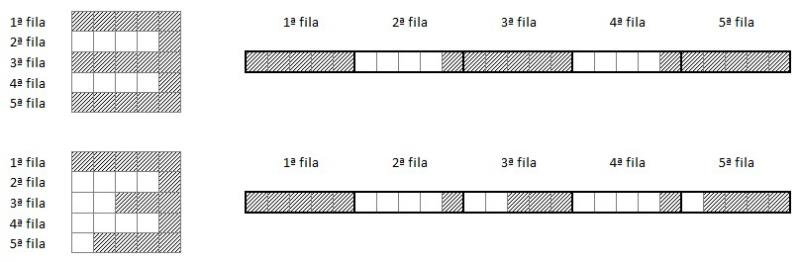
Si mostramos ambas muestras aplanadas una encima de otra, vemos muy fácilmente el alto número de píxels comunes:
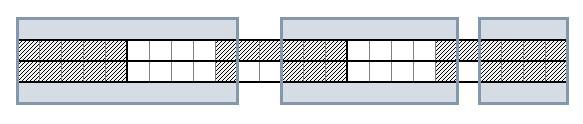
Sin embargo, si repetimos el mismo proceso con las imágenes correspondientes a los dígitos 2 y 4:
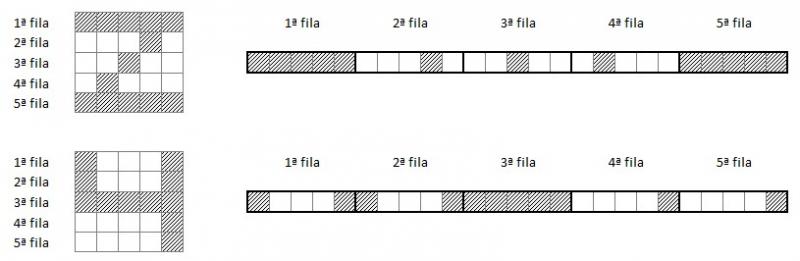
...y comparamos los resultados, comprobamos que, tal y como cabría esperar, los píxels comunes son muchos menos que en el caso anterior:

Todo esto nos indica que un clasificador tipo KNeighborsClassifier podría fácilmente distinguir unos dígitos de otros.
Nuevamente, estos ejemplos que estamos viendo son excesivamente idealizados y el dataset MNIST incluye imágenes de dígitos con mayor variabilidad, pero también aquí existen patrones que nos permitirían aplicar algoritmos de clasificación.
Probemos algunos de estos algoritmos en la práctica...