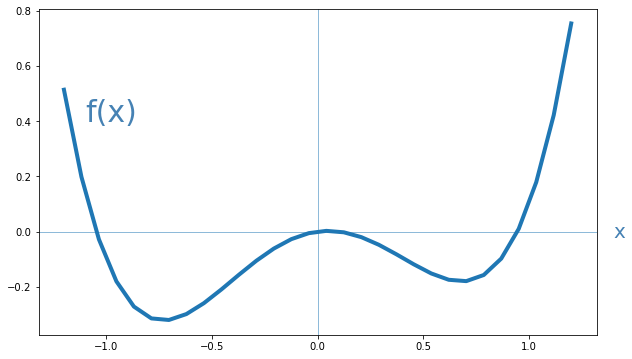
Una posible solución en la que podríamos pensar sería recurrir al cálculo infinitesimal. Para explicar este enfoque partamos de una función de una variable, f(x), con la siguiente representación gráfica:
Supongamos que esta función muestra el error cometido por una red neuronal con un único parámetro x (un peso o un bias). Se trata de un ejemplo absurdamente simple, pero nos sirve para entender el enfoque. Lo que querríamos sería encontrar el valor del parámetro x para el que la función (el error) toma un valor mínimo.
Sin entrar en su cálculo, la derivada de una función en un punto es el valor de su pendiente en dicho punto. Si la función crece, la derivada será positiva. Si decrece, será negativa. Y si la función es plana en un punto, su derivada será cero.
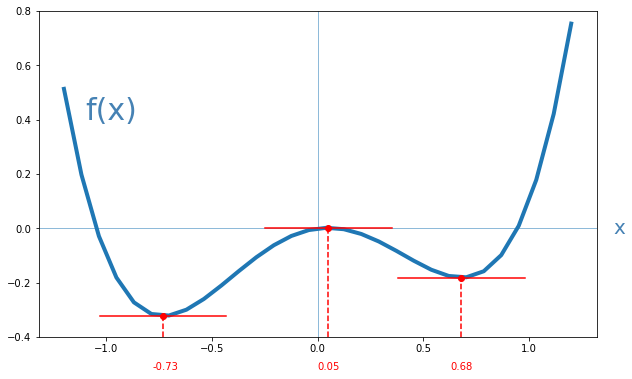
En la imagen anterior, la derivada de f(x) toma el valor 0 (pues la pendiente es nula) tanto en el valor -0.73, como en 0.05 y 0.68 (valores redondeados):
En esta última imagen vemos que los puntos de f(x) con derivada 0 son tanto los máximos como los mínimos de la función, tanto locales como globales.
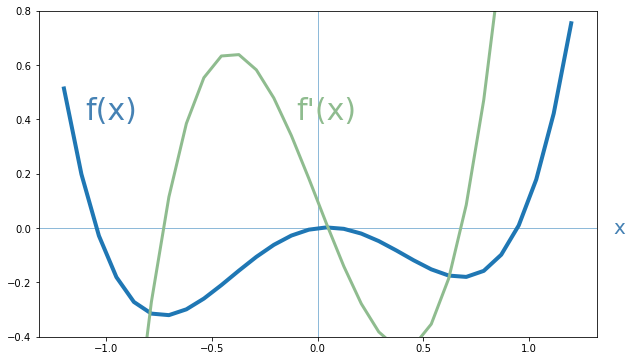
La función derivada de f(x), a la que podemos llamar f'(x) es una función que toma en cada valor de x la derivada de f(x) en dicho punto. En el caso de la función que nos ocupa, la gráfica de esta función derivada es la mostrada en verde en la siguiente imagen:
Podríamos identificar si los puntos de derivada 0 son máximos o mínimos calculando la derivada segunda de nuestra función f(x) (es decir, la función derivada de la función derivada): si la derivada segunda en uno de esos puntos es un valor positivo, se trata de un mínimo. Y si es un valor negativo, se trata de un máximo.
El método resulta claro, por lo tanto: Si tenemos una función f(x) (que depende de una única variable) para la que queremos calcular el punto en el que toma el valor mínimo, bastaría con calcular la derivada f'(x), y ver en qué puntos esta derivada toma el valor 0. Uno de esos puntos sería el valor buscado.
Pero recordemos que, en el ejemplo que estamos viendo, estamos suponiendo que la función f(x) representa el error cometido por nuestra red neuronal, y que ésta tiene un único parámetro (un peso o un bias) -ejemplo útil para entender el concepto, pero muy poco realista-. En un caso real, nuestra función de error puede tener cientos, miles o muchos más parámetros incluso. De hecho, las mayores redes neuronales que se usan hoy día llegan a involucrar miles de millones de parámetros.
Y el problema de este enfoque es que para funciones de muchas variables el cálculo de la derivada puede ser extremadamente complejo, si no imposible, pues implica el cálculo de lo que se conoce como derivadas parciales de la función con respecto a cada una de las variables. La fórmula resultante es, sencillamente, inmanejable.