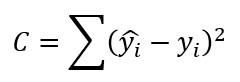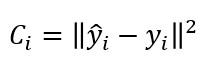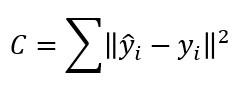También debemos reconsiderar la función de error o función de coste que vamos a utilizar en nuestro clasificador. Hasta ahora -para hacer más sencilla la interpretación de las explicaciones- hemos dado por supuesto que estábamos trabajando en un entorno de análisis de regresión considerando alguna variación de la siguiente función de coste:
En este escenario la predicción para una muestra i (ŷi) es un número, el valor objetivo o etiqueta (yi) es otro número, por lo que su diferencia elevada al cuadrado es otro número y el resultado del sumatorio también es un número.
En un escenario de clasificación resulta necesario retocar adecuadamente esta función, pues ahora tanto la predicción como el valor objetivo no son valores escalares, sino vectores. Ya vimos, por ejemplo, que si estamos trabajando con las imágenes de MNIST y la variable objetivo toma el valor 3 (de 10 clases posibles), esto supone que necesitamos alimentar nuestra red con un vector de 10 números que tomen el valor 0 menos el correspondiente a la clase "3", que deberá tomar el valor 1:
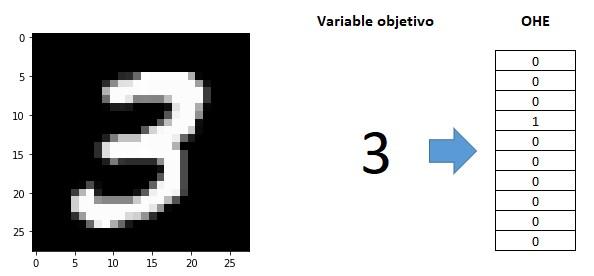
Y con la predicción ocurre exactamente lo mismo: el resultado devuelto por la red neuronal será un vector formado por 10 números indicando cada uno de ellos la "confianza" que la red tiene de que el valor representado en la imagen sea el correspondiente a cada clase.
Esto significa que, para el cálculo del error de una muestra, debemos enfrentar no dos números -como ocurría en el caso del análisis de regresión-, sino dos vectores.
Una solución para obtener este error es restar ambos vectores y obtener el módulo del resultado:
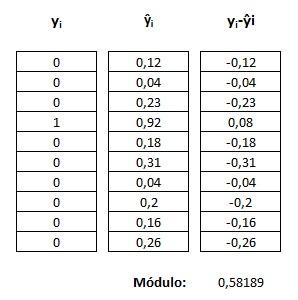
En la imagen anterior partimos de la variable objetivo correspondiente al número 3 (yi), nos inventamos una supuesta predicción (ŷi) y obtenemos la diferencia de ambos vectores (yi-ŷi). En la parte inferior se muestra el módulo de este último vector: 0.58189, obtenido como la raíz cuadrada de la suma de los cuadrados de los componentes del vector.
Este enfoque nos lleva a retocar la función de coste correspondiente a una muestra dejándola expresada de la siguiente manera:
(donde ||x̄|| representa el módulo del vector x̄)
...y definiendo, por lo tanto, la función de coste global con la siguiente expresión (o alguna variación de ésta):