Trabajando con una función de más de una variable, el concepto de derivada se generaliza en el concepto de gradiente. Al igual que la derivada, el gradiente representa la pendiente de la línea tangente a la función apuntando -al igual que ocurre con la derivada- hacia los valores crecientes.
Para visualizar el gradiente, volvamos a la función que ya hemos visto en secciones anteriores y fijémonos en un punto cualquiera (en negro en la imagen):
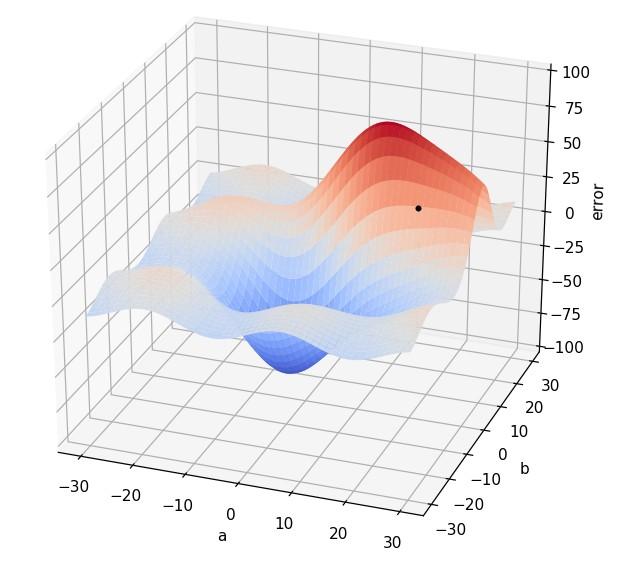
El punto escogido, a ojo, se corresponde con las coordenadas a = 15 y b = 20 (estos números no son relevantes para entender el concepto de gradiente).
Ahora imaginemos el plano tangente a la gráfica en dicho punto:
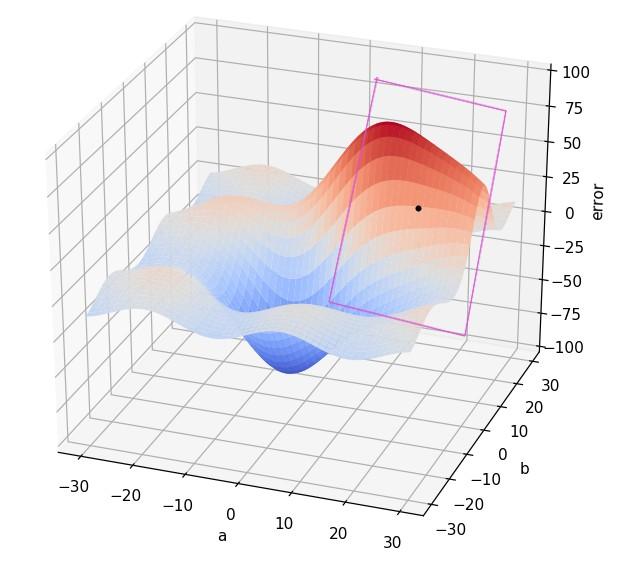
A continuación, fijémonos en la recta que, contenida en el plano anterior y pasando por nuestro punto, apunta en la dirección de mayor pendiente:
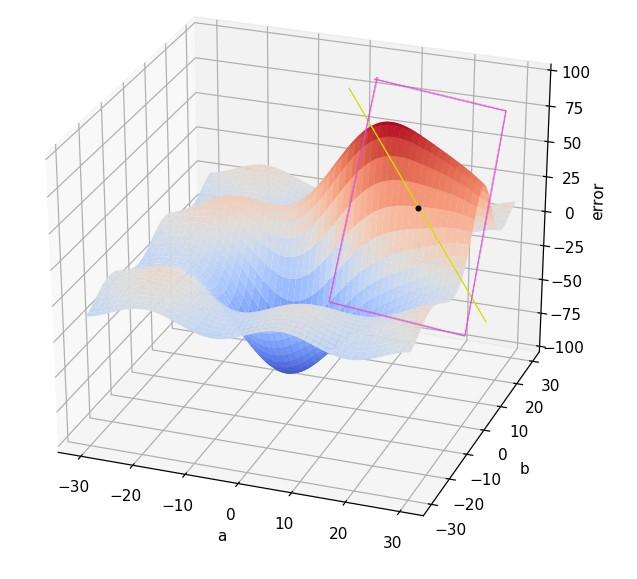
El gradiente es un vector que, partiendo de nuestro punto y sobre la recta anterior, apuntará en la dirección de mayor pendiente. Su módulo será igual a la pendiente de la recta con respecto al plano horizontal: Cuanto mayor sea la pendiente, mayor será la longitud del vector.
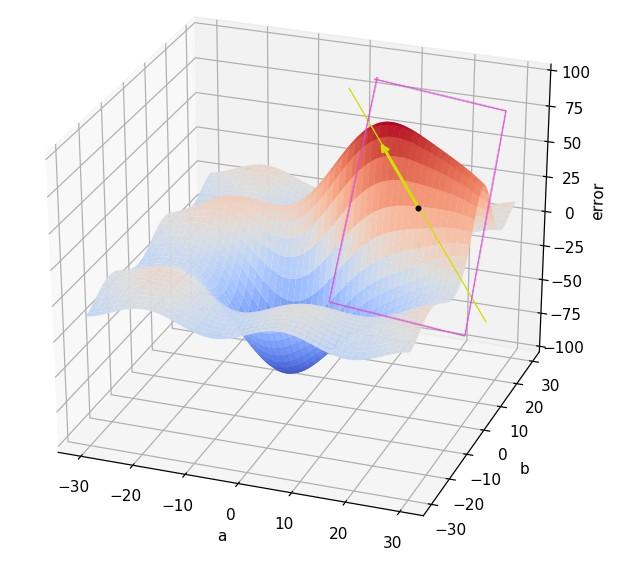
Para obtener este vector se calculan las derivadas parciales de la función con respecto a cada una de las variables de la función. Por ejemplo, si la función f depende de a y b, como en nuestro ejemplo, para un punto de la función (es decir, para una combinación dada de a y b), el gradiente estará formado por la derivada de la función con respecto a la variable a y por la derivada de la función con respecto a la variable b. Esto se representa formalmente de la siguiente forma:
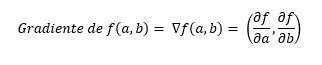
Esto supone que, si tenemos una función de dos variables a y b, el gradiente en un punto estará formado por dos valores: el primero representando la derivada parcial con respecto a la variable a, y el segundo representando la derivada parcial con respecto a la variable b. Si tuviésemos una función de 5 variables, el gradiente estaría formado por 5 valores, uno para cada variable.
En nuestro ejemplo estas derivadas parciales vendrían definidas por las pendientes de la función en el punto siendo analizado con respecto a las dos dimensiones definidas por a y b:
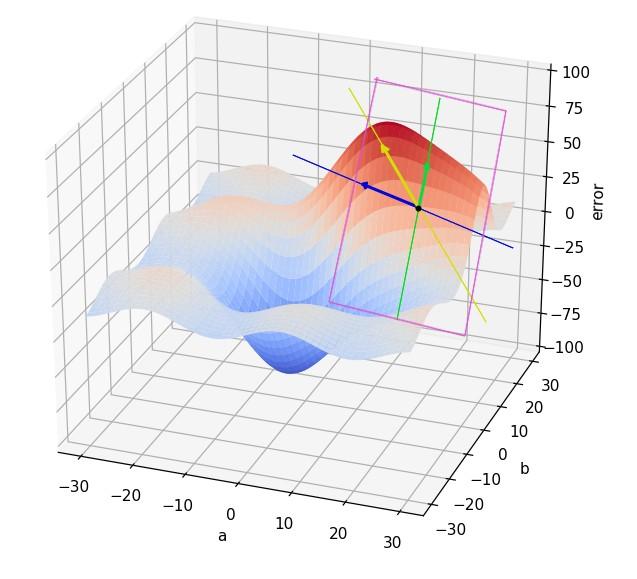
En esta imagen se muestra en verde la derivada parcial de la función con respecto a la variable b, y en azul la derivada parcial de la función con respecto a la variable a. Como puede verse, estos dos vectores (paralelos a los ejes) definen el vector gradiente.