Para ver el kernel trick en funcionamiento supongamos que la función Φ es la siguiente:
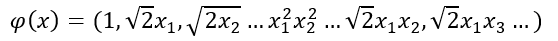
es decir, se trata de una transformación polinomial cuadrática que transforma un vector de n dimensiones en otro de n2.
Tal y como se ha comentado, tendríamos que transformar todos nuestros datos y calcular el producto escalar entre ellos para crear la matriz de Gram. Supongamos las muestras a y b. Las muestras transformadas serían las siguientes:
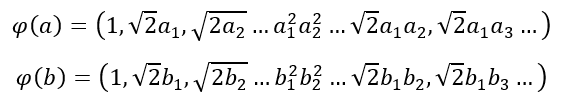
Y su producto escalar sería el siguiente:
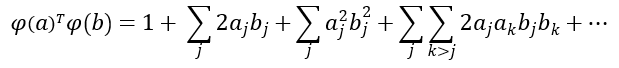
Sin embargo, si manipulamos el vector anterior, llegamos a una función extremadamente más simple:
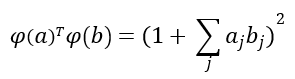
función que no depende más que de a y de b: calculamos el producto escalar de ambos vectores, sumamos 1 y elevamos al cuadrado. Y esto con independencia del número de características que la función Φ esté creando en el espacio destino.
Fijémonos una vez más en la expresión anterior: para calcular el producto escalar de los vectores transformados no necesitamos transformar los vectores. Basta con aplicar a los vectores a y b una función que solo depende de a y de b. Esta función es lo que llamamos kernel, y se representa habitualmente como K(a, b).