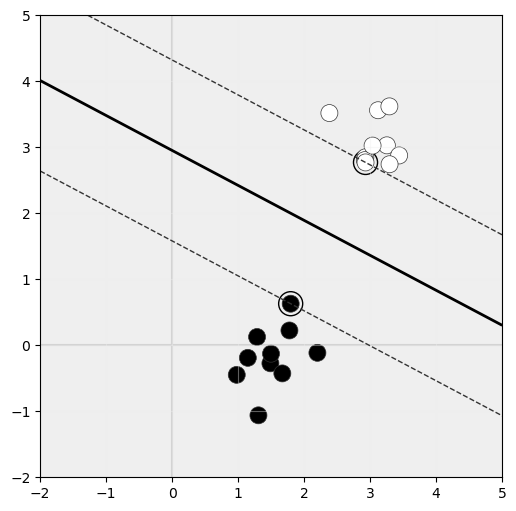
Veamos parte de las matemáticas que hay detrás del cálculo del hiperplano de máximo margen. Para ello, supongamos que partimos de un conjunto de muestras x acompañadas de la clase a la que pertenecen, y:
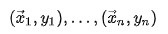
Y supongamos que tienen la siguiente distribución:
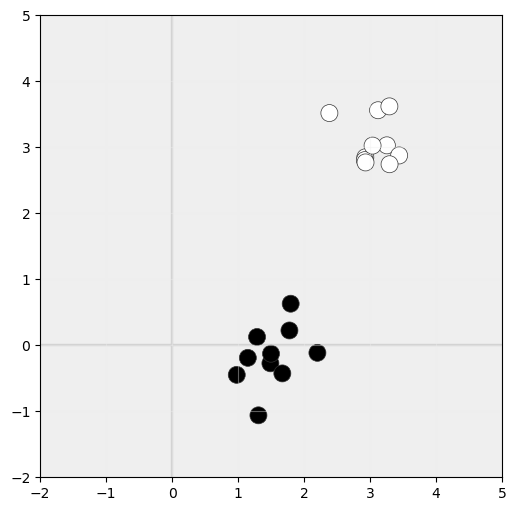
El hiperplano que buscamos es el siguiente: