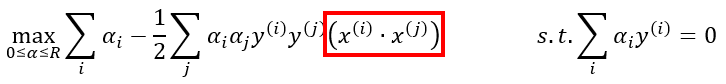Si hacemos las matemáticas, llegamos a la conclusión de que el margen vendrá dado por la siguiente expresión:
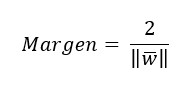
Con las restricciones vistas:
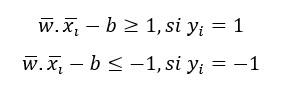
(recordemos que todavía no se ha obtenido ni el vector w ni el parámetro b que se ha añadido a las expresiones anteriores)
El objetivo es, por lo tanto, maximizar el margen con dichas limitaciones:
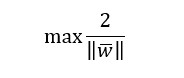
valor que coincide con el devuelto por la siguiente expresión:
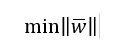
Y, en consecuencia, con la siguiente:
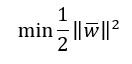
con las constricciones ya mencionadas.
Nos encontramos en un escenario de optimización cuadrática que permite aplicar un método denominado optimización de Lagrange, que une tanto la expresión a minimizar como las constricciones en una única expresión, en la que las constricciones van multiplicadas por unos valores (llamados multiplicadores de Lagrange) que termina adoptando la siguiente forma:
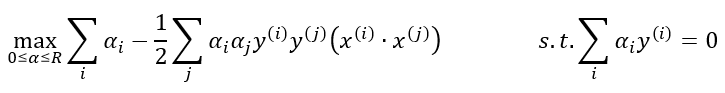
El primer término hace referencia al margen y el segundo a la penalización aplicada a las muestras mal clasificadas. Lo que nos interesa es comprobar que el resultado depende del producto escalar de todas nuestras muestras: