Si la función es convexa (si solo tiene un mínimo) podemos confiar en que el método visto funcione. Pero ¿qué ocurre si la función de error tiene más de un mínimo? Algunos pueden ser mínimos locales (no mínimos absolutos) en los que podríamos "caer", y el algoritmo de descenso de gradiente no sería capaz de salir de él. Otra situación interesante se da cuando a partir de dos puntos iniciales próximos sea posible llegar a dos mínimos distintos, como se ve en la siguiente imagen, en cuyo caso es cuestión de suerte llegar a uno o a otro:
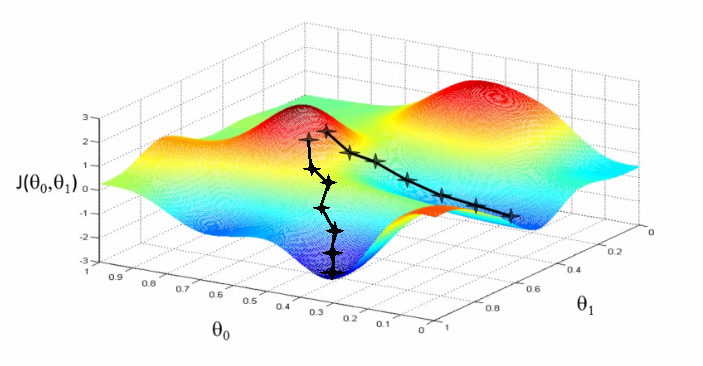
Debemos tener en cuenta, en todo caso, que cuando se entrena un modelo no se entrena una única vez con una única configuración. Se entrena cientos o miles de veces, con cientos o miles de configuraciones distintas, precisamente para evitar problemas como éstos. En el caso de la búsqueda de los parámetros óptimos (aquellos para los que el error de nuestro modelo sea mínimo) lo que haríamos sería aplicar el método de descenso de gradiente partiendo de muchos puntos (valores de los parámetros) iniciales, escogidos de forma más o menos aleatoria, con la esperanza de que, alguno de dichos puntos nos lleve encontrar el valor mínimo de la función de error (y los parámetros óptimos buscados).