Para entender el concepto de curva ROC (ROC curve, Receiver Operating Characteristic) tenemos que entender previamente cómo funciona un algoritmo de clasificación lineal como la regresión logística: A la hora de realizar una predicción, el modelo asigna una puntuación (un "score") a cada muestra del conjunto de pruebas. Este score se compara con un cierto valor límite ("threshold"). Si, para una muestra, su score es mayor que el threshold, se asigna a la clase principal. Si es menor, se asigna a la clase secundaria.
Siguiendo con el ejemplo visto relativo al Titanic, ya habíamos realizado la predicción:
prediction = model.predict(X_test)
prediction
array([0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1,
0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0,
1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1,
1, 0], dtype=int64)
Podemos ver el score que el modelo ha asignado a cada muestra con el método decision_function:
scores = model.decision_function(X_test)
scores
array([-1.94301282, -2.36213546, -1.21444007, 2.47651727, 1.1959797 ,
-0.60290339, 2.29157802, 2.53608913, -0.41796414, 0.95146859,
-2.59631885, 1.41196199, -2.15257414, 1.6564731 , 2.71070066,
0.53234595, -2.36213546, -1.71670281, -2.36213546, 0.90989925,
-1.48251942, 2.29157802, -2.15257414, -0.60290339, 0.53234595,
2.47651727, -2.36213546, 0.53234595, 1.6564731 , -0.65922644,
-1.94301282, 1.41196199, -2.36213546, -0.60290339, -2.59631885,
-0.18378075, -2.36213546, -1.48251942, -1.48251942, -1.48251942,
-0.41796414, -1.94301282, -2.36213546, -1.42400139, 2.05739463,
-2.36213546, -2.36213546, 1.99782277, -1.48251942, -0.83708678,
-0.60290339, 0.06073036, 1.1777786 , -2.36213546, -0.18378075,
-2.19539732, -0.60290339, -1.13792094, -0.94530689, -2.86545203,
-1.94301282, 0.77685706, 2.47651727, -0.18378075, 0.77685706,
-2.15257414, 2.29157802, -1.23800831, 1.1777786 , 2.29157802,
1.1777786 , -0.83708678, -0.41796414, -2.36213546, -2.36213546,
0.22038959, -1.79447578, -0.18378075, -2.36213546, -1.06339678,
-2.38675753, 0.01208211, 1.1777786 , -2.36213546, -1.48251942,
2.29157802, 2.71070066, 0.53234595, 1.41196199, -0.41796414])
Por defecto, el threshold aplicado es 0. Podemos ver esto fácilmente viendo, del array anterior, qué valores son mayores que 0 y cuáles son menores. Hagamos esto solo para los 10 primeros valores del array anterior:
scores[:10] > 0
...y comparemos este resultado con los 10 primeros valores de la predicción:
prediction[:10]
Vemos que se ha predicho un resultado de 0 (el pasajero no sobrevive) para aquellas muestras (para aquellos pasajeros) cuyos scores son menores que cero.
Pues bien, este clasificador con el threshold por defecto, supone un cierto True Positive Rate y un cierto False Positive Rate. Calculémoslos:
confusion_matrix(prediction, y_test)
array([[47, 9],
[ 4, 30]], dtype=int64)
Si extraemos los valores:
TPR = tp / (tp + fn)
TPR
FPR = (fp / (fp + tn))
FPR
Vamos a almacenar estos valores en sendas listas para poder acceder a ellos posteriormente.
TPRs = [TPR]
FPRs = [FPR]
Y aquí viene lo interesante: hemos dicho que se va a comparar cada score con el threshold. Si el valor es mayor que el threshold se asigna a la clase 1 (o principal), y si es menor, a la clase 0 (o secundaria). Veamos los scores, la predicción que estos scores suponen, y el "ground truth" (el valor real de la variable objetivo) añadiendo estos tres datos a un dataframe ordenando los scores de menor a mayor:
scores_df = pd.DataFrame({
"scores": scores,
"prediction": prediction,
"truth": y_test
})
scores_df.sort_values("scores", inplace = True)
Y mostremos ahora los scores que hay en torno al threshold de cero (se ha buscado manualmente su posición en el dataset):
scores_df.iloc[46:66]
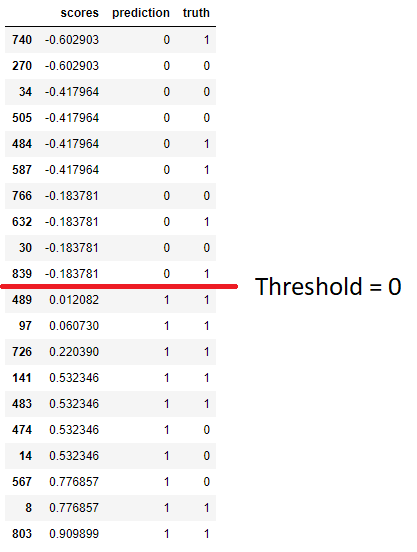
Lógicamente, todas las predicciones correspondientes a scores mayores que 0 aparecen con una predicción de 1, y al revés: las predicciones correspondientes a scores menores que cero aparecen con una predicción de 0.
Vemos, sin embargo, que el verdadero valor de la variable objetivo ("truth") no coincide siempre con la predicción. Lo ideal sería que por encima del threshold solo hubiese muestras de la clase 1 (para tener un TPR de 1), así que ¿qué ocurriría si en lugar de un threshold de 0 considerásemos un threshold de 0.8? En la imagen anterior vemos que, moviendo el threshold hasta dicho valor, estaríamos pasando tres muestras cuyo valor verdadero es 0 al bloque de "predicción 0". Es decir, estaríamos mejorando el TPR de nuestro modelo (al disminuir el número de falsos negativos)... pero a costa de empeorar el FPR. Vamos a calcular estos valores. Para ello tenemos los scores, de forma que podemos realizar la predicción "a mano":
new_prediction = scores > 0.8
new_prediction
array([False, False, False, True, True, False, True, True, False,
True, False, True, False, True, True, False, False, False,
False, True, False, True, False, False, False, True, False,
False, True, False, False, True, False, False, False, False,
False, False, False, False, False, False, False, False, True,
False, False, True, False, False, False, False, True, False,
False, False, False, False, False, False, False, False, True,
False, False, False, True, False, True, True, True, False,
False, False, False, False, False, False, False, False, False,
False, True, False, False, True, True, False, True, False])
confusion_matrix(new_prediction, y_test)
array([[50, 15],
[ 1, 24]], dtype=int64)
TPR = tp / (tp + fn)
TPR
FPR = (fp / (fp + tn))
FPR
Tal y como sospechábamos, el TPR del modelo ha aumentado hasta el 96%, pero el FPR ha aumentado también (lo que significa que hay más falsos positivos que antes).
Almacenemos estos valores en las listas que habíamos creado:
TPRs.append(TPR)
FPRs.append(FPR)
Y, en el ejemplo visto, hemos aumentado el threshold hasta 0.8. Si -nuevamente, viendo los scores- disminuimos el threshold hasta -0.5, vemos que estaríamos "sacando" del bloque de muestras que recibe una predicción 0 varias muestras cuyo valor real es 1... pero también estaríamos moviendo varias muestras que ahora mismo están bien clasificadas. Es decir, estaríamos mejorando el FPR (disminuyendo el número de falsos positivos) a costa de empeorar el TPR:
new_prediction = scores > -0.5
new_prediction
array([False, False, False, True, True, False, True, True, True,
True, False, True, False, True, True, True, False, False,
False, True, False, True, False, False, True, True, False,
True, True, False, False, True, False, False, False, True,
False, False, False, False, True, False, False, False, True,
False, False, True, False, False, False, True, True, False,
True, False, False, False, False, False, False, True, True,
True, True, False, True, False, True, True, True, False,
True, False, False, True, False, True, False, False, False,
True, True, False, False, True, True, True, True, True])
confusion_matrix(new_prediction, y_test)
array([[43, 5],
[ 8, 34]], dtype=int64)
tn, fp, fn, tp = confusion_matrix(new_prediction, y_test).flatten()
TPR = tp / (tp + fn)
TPR
FPR = (fp / (fp + tn))
FPR
Volvamos a almacenar los valores calculados:
TPRs.append(TPR)
FPRs.append(FPR)
También ahora hemos confirmado nuestras sospechas: hemos mejorado el FPR (disminuyéndolo) pero a costa de empeorar el TPR.
Llevemos a la gráfica de TPR vs. FPR las tres parejas de valores encontrados:
t = ["0", "0.8", "-0.5"]
fig, ax = plt.subplots(figsize = (6, 6))
ax.set_xlabel("False Positive Rate", fontsize = 15)
ax.set_ylabel("True Positive Rate", fontsize = 15)
ax.set_xticks(np.linspace(0, 1, 11))
ax.set_yticks(np.linspace(0, 1, 11))
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
sns.scatterplot(x = FPRs, y = TPRs, s = 50);
for i in range(len(t)):
plt.text(FPRs[i] + 0.02, TPRs[i] - 0.03, t[i], color = "red", fontsize = 15)
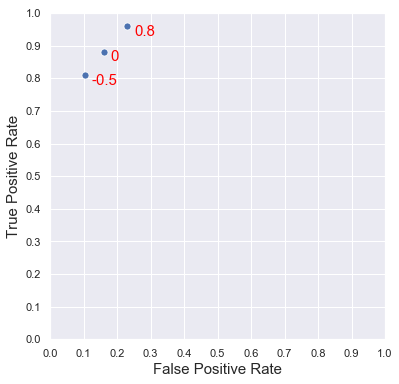
...gráfica que muestra exactamente las variaciones que hemos visto.
Hemos probado tres valores del threshold. Vamos a probar todos los thresholds desde el valor mínimo del score hasta el valor máximo, a ver cuál es el resultado:
TPRs = []
FPRs = []
for threshold in np.sort(scores):
new_prediction = scores > threshold
tn, fp, fn, tp = confusion_matrix(y_test, new_prediction).flatten()
TPR = tp / (tp + fn)
FPR = fp / (fp + tn)
TPRs.append(TPR)
FPRs.append(FPR)
Ahora ya tenemos los TPR y FPR en las listas TPRs y FPRs. Mostrémoslas en una gráfica etiquetando cada punto con el threshold al que se corresponde:
fig, ax = plt.subplots(figsize = (10, 10))
ax.set_xlabel("False Positive Rate", fontsize = 15)
ax.set_ylabel("True Positive Rate", fontsize = 15)
ax.set_xticks(np.linspace(0, 1, 11))
ax.set_yticks(np.linspace(0, 1, 11))
sns.scatterplot(x = FPRs, y = TPRs, s = 40);
plt.plot([0, 1], [0, 1], 'k--')
for i in range(len(scores)):
score_i = np.sort(scores)[i]
if score_i > -0.65:
ax.text(FPRs[i] + 0.012, TPRs[i] - 0.004, round(score_i, 2), color = "red", fontsize = 12)
else:
if i % 4 == 0:
ax.text(FPRs[i] - 0.01, TPRs[i] - 0.03, round(score_i, 2), color = "red", fontsize = 12)
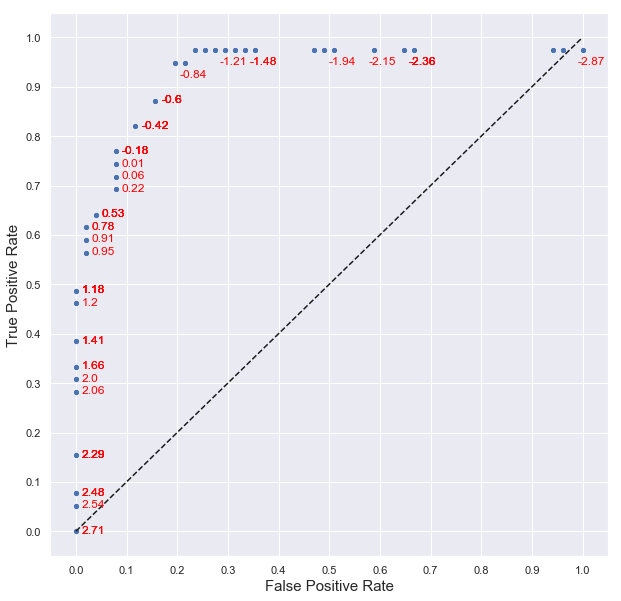
Lo que estamos viendo es exactamente la curva ROC del clasificador. Y nos da bastante información: en primer lugar nos dice que aumentando o disminuyendo lo suficiente el threshold podemos conseguir que nuestro algoritmo de clasificación alcance un TPR o un FPR casi perfecto. El único "pero" es que lo conseguiremos a costa de empeorar la otra métrica. Esto significa que, una vez creado el modelo, podemos configurarlo en función de nuestros intereses fijando un threshold u otro (para conseguir un mayor TPR o un FPR). Por otro lado, cuanto más se aproxime la gráfica al punto (0, 1), más se comportará como un clasificador ideal. En la gráfica anterior se muestra la línea diagonal que marca el comportamiento de los clasificadores que tienen tantos verdaderos positivos como falsos negativos, y tantos verdaderos negativos como falsos positivos.