Al igual que hemos definido el True Positive Rate (recall o exhaustividad) como el ratio entre el número de verdaderos positivos y el número de positivos (reales), el False Positive Rate se define como el ratio entre el número de falsos positivos y el número de negativos (reales). Lógicamente, el clasificador ideal tendría un FPR de cero (pues no tendría falsos positivos), y el peor clasificador posible tendría un FPR de uno (todos los negativos reales serían identificados erróneamente como positivos):
y_real = [1, 1, 1, 1, 1, 1, 1, 0, 0, 0]
y_pred = [1, 1, 1, 1, 0, 0, 0, 0, 1, 1]
En este ejemplo que ya habíamos usado para el cálculo del TPR tenemos 10 elementos de los que 7 son positivos y 3 son negativos. Hemos marcado en nuestra predicción como positivos 6 elementos, de los que 4 son verdaderos positivos y 2 son falsos positivos. De forma semejante, hemos marcado 4 negativos, de los que 1 es un verdadero negativo y los otros 3 son falsos negativos.
La matriz de confusión devuelta por sklearn es:
confusion_matrix(y_real, y_pred)
array([[1, 2],
[3, 4]], dtype=int64)
El FPR se calcula, tal y como acabamos de comentar, como el ratio entre verdaderos negativos y el número de negativos: 2 / 3, y representa la proporción de negativos que no estamos identificando. Mostrando este cálculo en la matriz de confusión (ordenada según el criterio más habitual) sería:
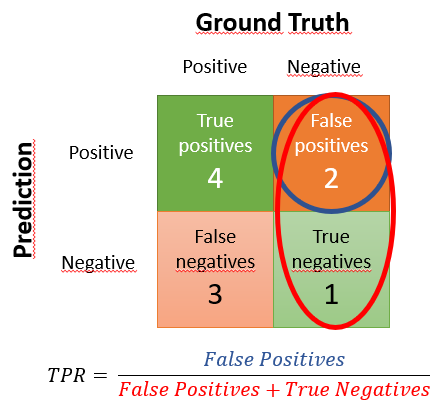
Es decir, 2/3.