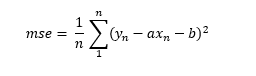Un aspecto al que no hemos dado mucha importancia al hablar del algoritmo de Descenso de Gradiente es el siguiente: si la función de error es el error cuadrático medio, ya comentamos que -siguiendo con el ejemplo de la recta de regresión ax + b, podríamos escribir la función de coste de la siguiente manera:
Aun cuando calcular las derivadas parciales con respecto a las variables a y b resulte sencillo para un ordenador, en la fórmula anterior estamos involucrando en el cálculo las n muestras de nuestro conjunto de entrenamiento. Es decir, para calcular los incrementos de cada parámetro en el algoritmo de Descenso de Gradiente habría que hacer pasar todos los datos por el modelo (por ejemplo, por la Adaline) y calcular las derivadas parciales. Y esto para calcular un único incremento de los parámetros. Para alcanzar el mínimo de la función tendríamos que repetir el proceso el número de veces que fuese necesario. Y el número de datos n puede ser un muy grande, lo que podría suponer un procedimiento muy costoso desde un punto de vista computacional (y requerir mucho tiempo, mucha memoria, etc.).
El optimizador Stochastic Gradient Descent (SGD) o Descenso de Gradiente Estocástico simplifica el cálculo considerando solo una muestra antes de obtener las derivadas parciales. Esto supone que las derivadas parciales obtenidas no van a ser “óptimas”, es decir, no van a apuntar en la dirección de mayor descenso de la función de error, pero este problema se compensa con el mayor número de modificaciones a los parámetros que se aplican, lo que lleva a tiempos de entrenamiento mucho menores:
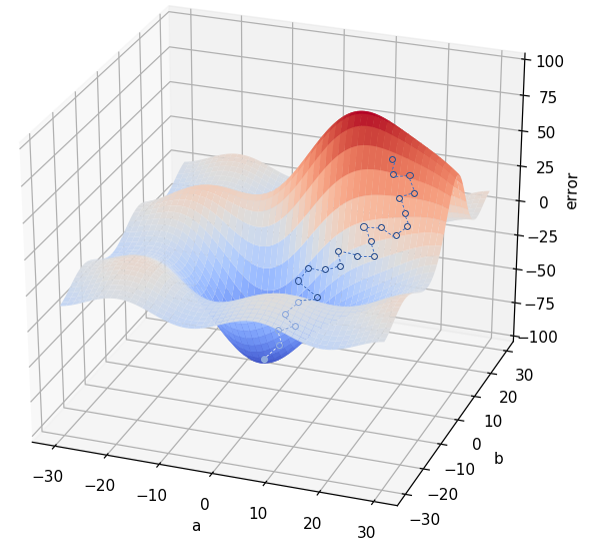
Tal y como se muestra en la imagen anterior, el camino que nos lleva desde la pareja de parámetros (a, b) inicial hasta los valores óptimos es ahora mucho más errático, aunque, como se ha comentado, el cálculo de dichos incrementos es ahora mucho más sencillo.
Una ventaja de este comportamiento errático es que puede resultarle más sencillo al algoritmo el escapar de un mínimo local.