Es por todo esto que, en lugar de intentar aplicar "una fórmula" que nos devuelva directamente los valores de los parámetros que minimizan el error, se recurre a métodos que, de forma iterativa, se aproximen a dichos valores.
Para entender este enfoque, supongamos ahora que estamos trabajando con una red neuronal con dos parámetros (un peso y un bias, o dos pesos...). Nuevamente se trata de un ejemplo muy poco real, pero perfecto para plantear el enfoque. Llamemos a esos parámetros a y b.
Supongamos que, para tener una idea de cómo se ve afectado el error según los valores de a y b que se escojan, generamos muchas parejas de valores (a, b), que calculamos el error correspondiente a cada combinación y que mostramos el resultado en una gráfica tridimensional en la que los valores a y b se muestran en el plano horizontal y el error correspondiente en el eje vertical:
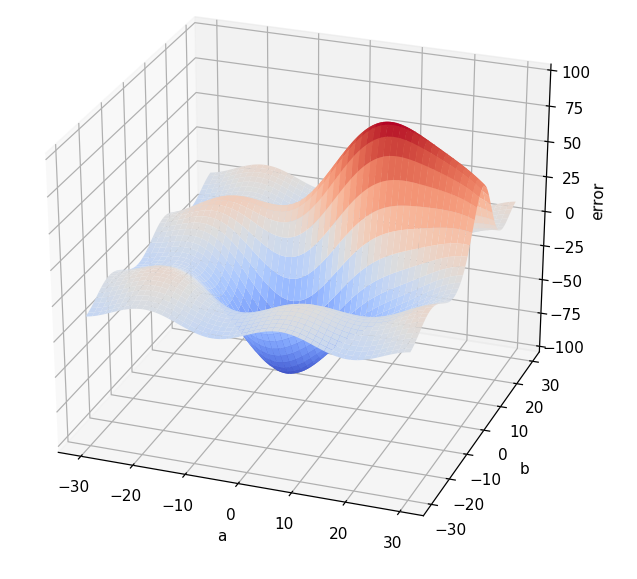
Todo parece indicar que hay una combinación de valores a y b que generan el menor error posible y, a ojo, parece que esta combinación está cerca de a = 0 y b = 0.
El objetivo, tal y como se ha comentado, es averiguar la combinación de a y b para la que el error toma el valor más bajo posible sin recurrir al cálculo infinitesimal, sino a un método iterativo que va a ir calculando estos valores aproximándose a ellos cada vez más en cada iteración. A este método es a lo que denominamos optimizador.