Aun así, restar la derivada parcial supone, en cualquier caso, restar una cantidad demasiado grande. Si estamos en el punto en el que la variable a toma el valor 10 y en dicho punto la derivada parcial con respecto a a vale 7, restar a a el valor 7 supondría pasar a de 10 a 3. Eso es un salto demasiado grande: no sabemos qué forma tiene nuestra función de error entre dichos valores, tal vez tenga un mínimo que estemos saltando. Así que lo que hacemos es multiplicar las derivadas parciales por una pequeña cantidad, cantidad a la que denominamos tasa de aprendizaje o learning rate, concepto que ya se ha comentado en secciones anteriores.
Si la tasa de aprendizaje vale 0.001, por ejemplo, y la derivada parcial calculada era 7, esto supondría restar al parámetro a 7 x 0.001 = 0.007. Es decir, a pasaría de valer 10 a valer 9.993. Esto sí que es un pequeño paso hacia la dirección del valor mínimo de la función. Con la variable b habría que hacer lo mismo, claro. Los incrementos de a y de b quedarían, por lo tanto, de la siguiente forma:
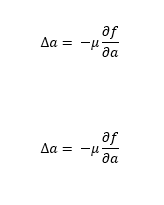
...donde μ es la tasa de aprendizaje.