Ya se ha comentado que un kernel va a aplicar una función de transformación φ a nuestros datos, de forma que al transformarlos desde un espacio de baja dimensionalidad:
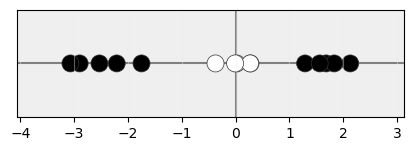
a otro de alta dimensionalidad:
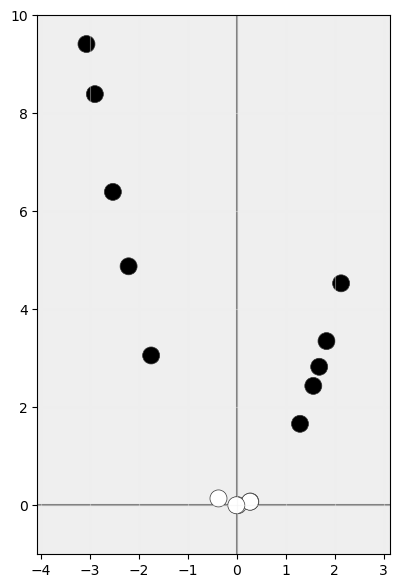
sea más fácil encontrar un clasificador lineal:
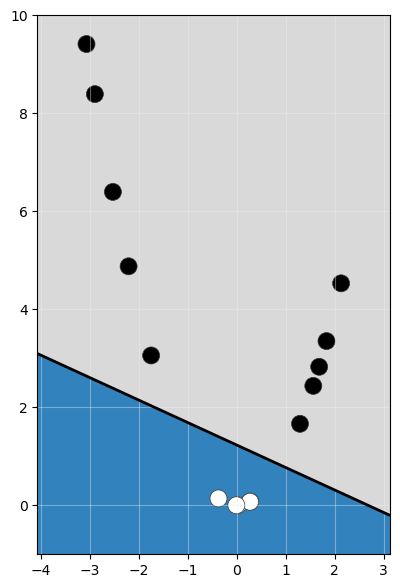
Esto nos obliga a transformar nuestros datos originales x al nuevo espacio aplicando la función de transformación φ(x).
Pues bien, si transformamos los datos y aplicamos el mismo proceso matemático para encontrar el hiperplano de máximo margen en el nuevo espacio, volveremos a obtener una función objetivo semejante a la vista:
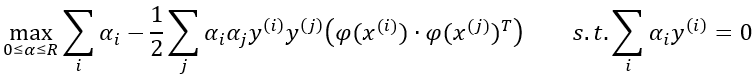
función que también depende del producto escalar de los vectores transformados:
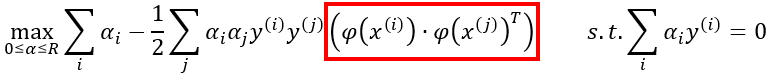
Es decir, en la práctica, sea cual sea la transformación a aplicar a los datos, la función objetivo a resolver para obtener el hiperplano de máximo margen depende del producto escalar de los vectores transformados, productos escalares que se involucran en la función en forma de una matriz cuyo cálculo puede resultar muy exigente desde un punto de vista computacional, más si el espacio de los vectores transformados es de muy alta dimensionalidad, y más si el número de muestras con las que estamos trabajando es elevado.
Por ejemplo, esto supone que si estamos trabajando con 10 mil muestras (que no es una cifra que podamos calificar de elevada), cada muestra con 20 características predictivas (es decir, estamos trabajando en un espacio de 20 dimensiones) y queremos transformar nuestros datos a un espacio de, por ejemplo, 100 dimensiones, tendríamos que transformar las 10 mil muestras y calcular el producto escalar de 10.000 * 10.000 vectores de 100 dimensiones cada uno. Es decir, 100 millones de cálculos.
Esto es mucho trabajo.
Y estamos considerando un espacio de alta dimensionalidad de "solo" 100 dimensiones, pues, por ejemplo, hay transformaciones que convierten nuestros datos a un espacio ¡con un número infinito de dimensiones!
y aquí es donde entra el juego el llamado kernel trick (truco del kernel).