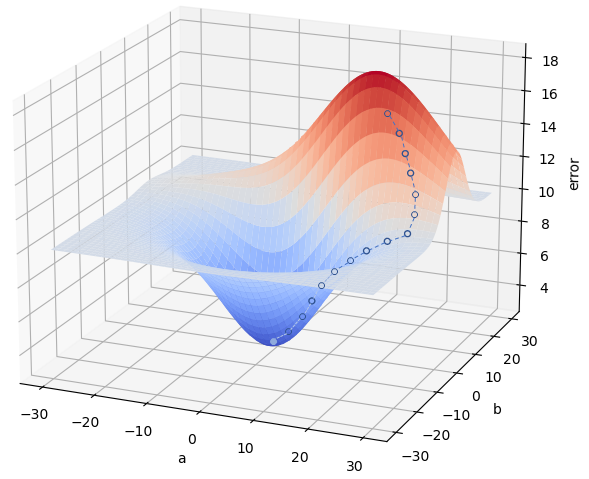
El algoritmo de Gradient Descent o Descenso de Gradiente en español -también conocido como Batch Gradient Descent- se basa en la siguiente idea:
Si escogemos una pareja aleatoria de valores a y b es posible calcular el error que estamos cometiendo. Y, si se cumplen ciertas condiciones, es posible calcular, para ese punto en concreto, cuál es la pendiente de la función de error. La metáfora que suele utilizarse para esto es imaginar que estamos de noche en medio de una montaña y que el objetivo es alcanzar el punto más bajo. Si nos han dejado en un punto aleatorio, siempre podemos ver que, en algunas direcciones, el terreno sube -lo que no nos conviene, pues el objetivo es bajar- y que en otras baja -lo que aparenta ser más conveniente-. Y, de entre las direcciones que bajan, podemos escoger aquella en la que el descenso es más pronunciado. Así que damos un paso en dicha dirección. Y volvemos a plantearnos la situación: desde el nuevo punto en el que estamos, ¿cuál es la dirección en la que el terreno desciende más rápidamente? Y volvemos a dar un paso en dicha dirección. Y repetimos el proceso hasta que lleguemos a un punto en el que todas las direcciones nos lleven hacia arriba, es decir, cuando hayamos llegado a un mínimo.
Veamos este mismo proceso en nuestro ejemplo de la recta de regresión. Hemos escogido una pareja de valores a y b aleatorios (supongamos que son a = 15 e y = 20), calculamos el error en dicho punto y la pendiente de la función de error. Determinamos, por ejemplo, que hay una dirección en la que el terreno sube con la mayor pendiente posible (flecha roja en la siguiente imagen) y que hay otra en la que la pendiente es la menor posible (flecha verde):
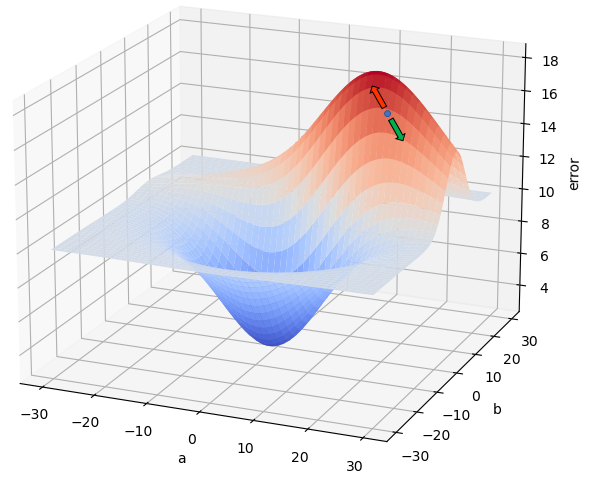
De forma que modificamos nuestros valores iniciales a y b "en la dirección de la flecha verde". Esto puede significar que a pase, por ejemplo, de 15 a 16, y que b pase de 20 a 19. En el nuevo punto, volvemos a comprobar cuál es la pendiente a nuestro alrededor:
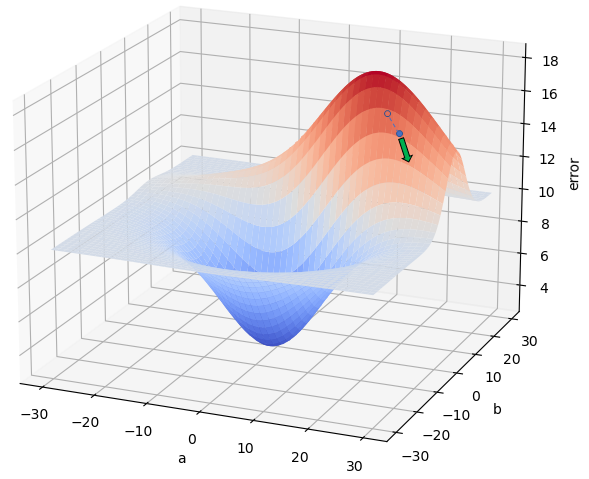
Una vez identificada la dirección con menor pendiente (flecha verde en la anterior imagen), volvemos a actualizar los valores de a y b en la dirección de mayor pendiente, para pasar a -por ejemplo- de 16 a 16.5 y b de 19 a 18.
Este proceso se repite hasta que se alcance un punto en el que no sea posible modificar los valores de a y b disminuyendo el error, momento en el que habremos alcanzado un mínimo de la función: