La función HEXBINY mapea unas coordenadas x e y al hexágono más próximo, devolviendo la coordenada y del centro de éste.
HEXBINY(
x,
y
)
- x: coordenada x del punto a mapear.
- y: coordenada y del punto a mapear.
La función HEXBINY devuelve un número real o entero, representando la coordenada y del centro del hexágono más próximo al punto (x, y).
Los hexágonos con los que se mapean las coordenadas x e y tienen lados de longitud 1, por lo que puede resultar necesario escalar las coordenadas originales para adaptarlas adecuadamente.
Podemos calcular la coordenada y del centro del hexágono dentro del cual caería el punto (1, 1) con el siguiente campo calculado:
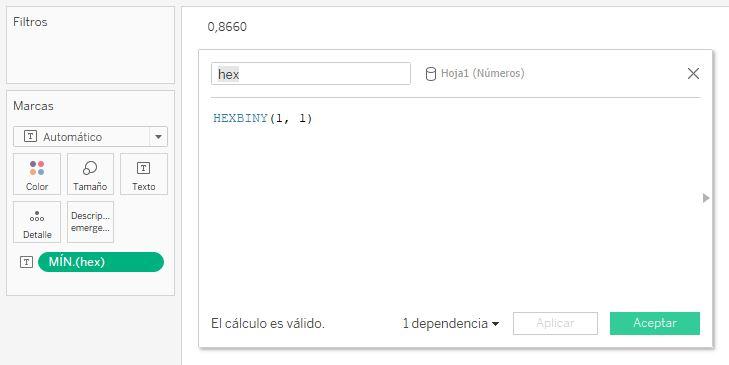
hex =
HEXBINY(1, 1)
Si llevamos el campo calculado al lienzo y cambiamos la función de agregación que se aplica por defecto (SUM) a MIN, por ejemplo, obtenemos el siguiente resultado:
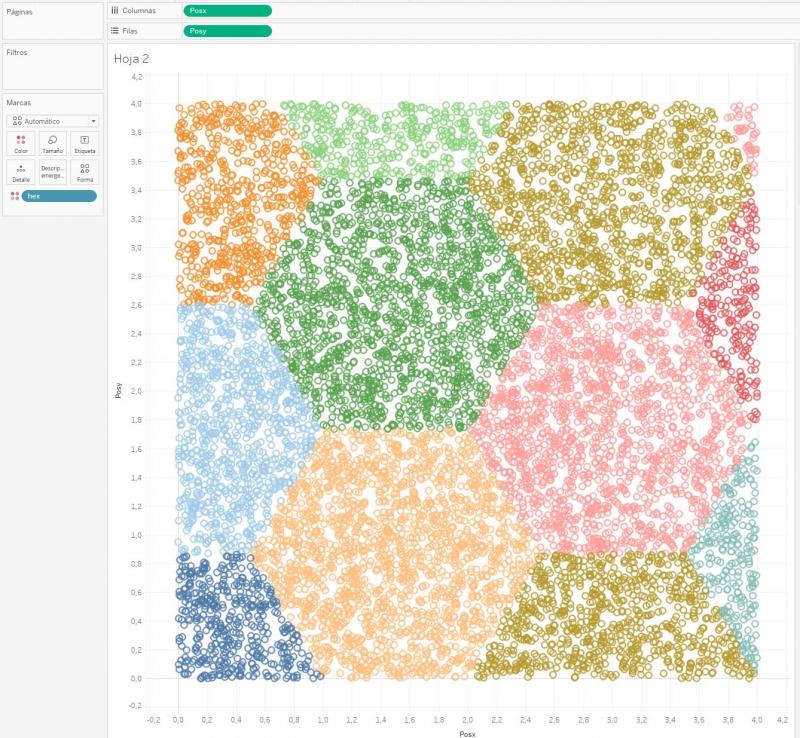
Para visualizar los hexágonos, vamos a generar varios miles de puntos aleatorios entre los valores (0, 0) y (3, 3), mostrarlos en un gráfico de dispersión, y aplicar el mismo color a aquellos que caigan en el mismo hexágono. Partimos de la tabla aleatoria de puntos creada con Excel:
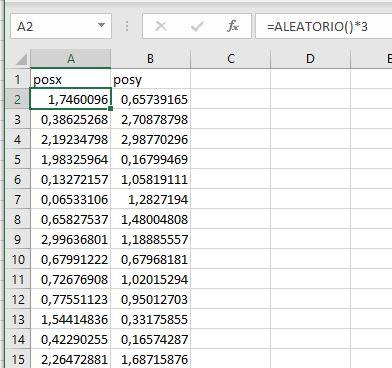
A continuación vamos a calcular las coordenadas x e y de los centros de los hexágonos a los que se asociaría cada punto, para lo que vamos a recurrir a un par de campos calculados:
hex_x =
HEXBINX([Posx], [Posy])
hex_y =
HEXBINY([Posx], [Posy])
Si llevamos el resultado a una tabla, obtenemos lo siguiente:
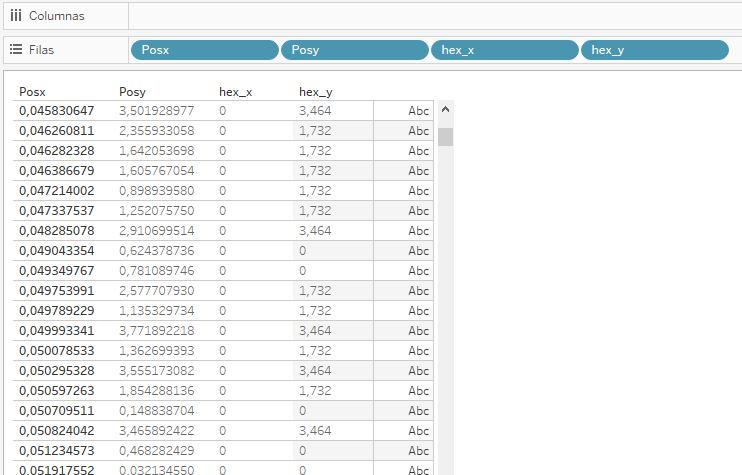
En el listado anterior vemos que la coordenada x es cero para todos los puntos mostrados, lo que es lógico si consideramos que el listado anterior está ordenado según la coordenada x de los puntos y la imagen muestra los más próximos a cero.
Con esto ya sabemos a qué hexágono se asocia cada punto, pero si quisiéramos mostrar los puntos de colores distintos en función del hexágono asociado, tendríamos que poder distinguir unos hexágonos de otros. Aprovechando las coordenadas ya calculadas de los centros, podemos crear un nuevo campo calculado que concatene la parte entera de dichas coordenadas. Por ejemplo, al hexágono de coordenadas (0, 1.732) le daríamos la etiqueta "01", y al hexágono de coordenadas (3, 3.464) le daríamos la etiqueta "33":
hex =
STR(INT([hex_x])) + STR(INT([hex_y]))
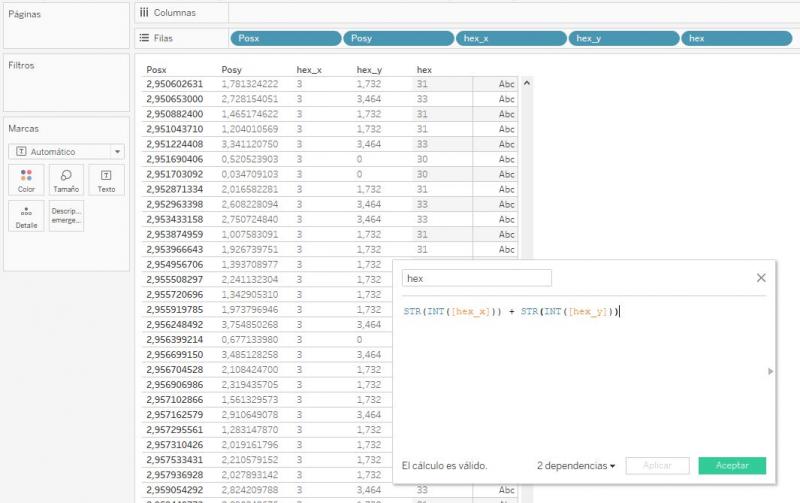
Ahora ya podemos crear nuestro gráfico de dispersión y llevar el campo calculado hex a la sección Color de la tarjeta de marcas, mostrándose cada punto del color asociado a cada hexágono: