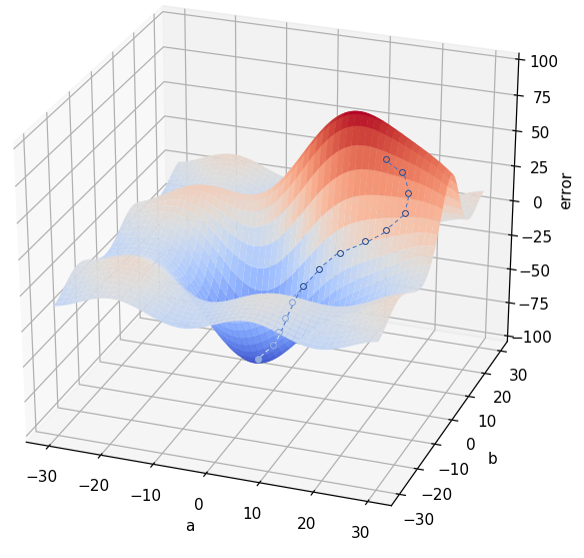
El algoritmo de Gradient Descent (pues se trata de un algoritmo, aunque no de Machine Learning), o Descenso de Gradiente en español -también se lo conoce como Batch Gradient Descent por motivos que veremos en breve- se basa en la siguiente idea:
Si escogemos una pareja de valores a y b aleatorios es posible calcular el error que estamos cometiendo (haciendo pasar nuestros datos de entrenamiento por la red, comparando el resultado devuelto por la red con la etiqueta de cada muestra y -en nuestro ejemplo- sumando los errores de todas las muestras). Y supongamos que es posible calcular, para ese punto de la función de error asociado a la combinación de parámetros a y b en concreto, cuál es la pendiente del error alrededor del punto.
La metáfora que suele utilizarse para explicar este método es imaginar que estamos de noche en medio de una montaña y que el objetivo es alcanzar el punto de menor elevación. Si nos han dejado en un punto aleatorio siempre podemos ver que, en algunas direcciones, el terreno sube -lo que no nos conviene pues el objetivo es bajar- y que en otras baja -lo que nos conviene más-. Y, de entre las que bajan, podemos escoger aquella dirección en la que el descenso sea más pronunciado con la esperanza de que nos lleve al punto de menor elevación y lo haga de la forma más rápida posible. Así que damos un paso en dicha dirección. Y volvemos a plantearnos la situación: desde el nuevo punto en el que estamos ¿cuál es la dirección en la que el terreno baja más rápidamente? Y volvemos a dar un paso en dicha dirección. Y repetimos el proceso hasta que lleguemos a un punto en el que no sea posible seguir bajando, es decir, cuando hayamos llegado a un mínimo.
Veamos este mismo proceso en nuestro ejemplo de red neuronal con dos parámetros. Hemos escogido una pareja de valores a y b aleatorios (supongamos que son a = 15 e y = 20), calculamos el error en dicho punto y vemos la pendiente de la función de error a nuestro alrededor (veremos más adelante cómo se realiza este cálculo). Determinamos, por ejemplo, que hay una dirección que implica un sentido en el que el terreno sube con la mayor pendiente posible (flecha roja en la siguiente imagen) y el sentido opuesto en el que la pendiente es la menor posible (flecha verde):
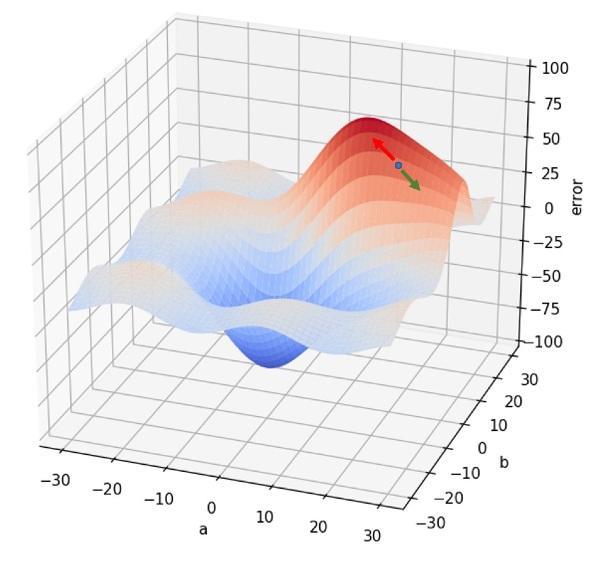
De forma que modificamos nuestros valores iniciales a y b "en el sentido de la flecha verde". Esto puede significar que a pase de 15 a 16 (por ejemplo), y que b pase de 20 a 19. En el nuevo punto, volvemos a comprobar cuál es la pendiente a nuestro alrededor:
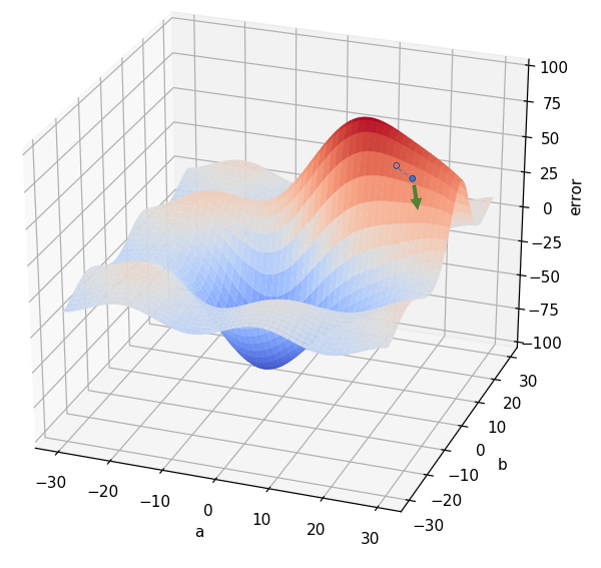
Una vez identificado el punto con menor pendiente (flecha verde en la anterior imagen), volvemos a actualizar los valores de a y b en la dirección adecuada, para pasar a -por ejemplo- de 16 a 16.5 y de 19 a 18.
Este proceso se repite hasta que se alcance un punto en el que no sea posible modificar a y b disminuyendo el error: