Habíamos visto que, dada una neurona artificial -supongamos que sigmoide-, podíamos obtener la salida de la misma aplicando la función de activación al producto escalar del vector formado por los valores de entrada y el vector de pesos, más el bias:
salida = σ(w•x + b)
Si queremos obtener la salida de una capa de la red (en el ejemplo de la siguiente imagen, los valores a1 e a2 correspondientes a la única capa oculta de la red neuronal):
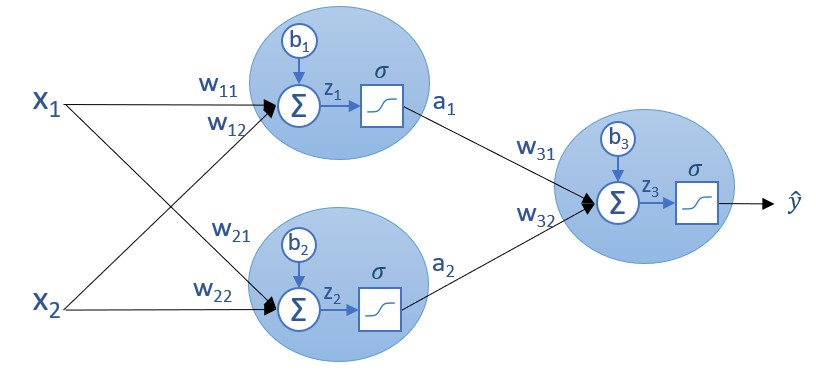
...podríamos hacerlo valor por valor:
[1] a1 = σ(z1) = σ(w11*x1 + w12*x2 + b1)
[2] a2 = σ(z2) = σ(w21*x1 + w22*x2 + b2)
Sin embargo, no debemos olvidar que, en este ejemplo, estamos considerando apenas dos características predictivas y una capa oculta de dos neuronas, por lo que, en casos más complejos, este enfoque resultaría bastante menos útil.
Hay, sin embargo, un método que nos permite obtener la salida de una capa de una forma mucho más elegante y ordenada. Este método consiste en representar los valores de entrada a la capa, los pesos y los bias como matrices, y recurrir a operaciones entre éstas para obtener una matriz de salida de la capa, matriz que estará formada por los valores que queremos obtener.
Concretamente, si expresamos el conjunto de valores de entrada a la capa como una matriz de tamaño (n, 1) -es decir, n filas y una columna, siendo n el número de valores de entrada- y llamamos al resultado x:
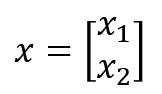
...expresamos el conjunto de pesos de los enlaces que llegan a una capa como una matriz de tantas filas como neuronas tenga la capa y tantas columnas como valores de entrada a la capa existan, y llamamos al resultado W:
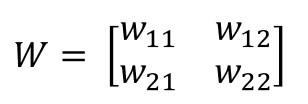
...y, por último, expresamos el conjunto de bias como una matriz de tamaño (m, 1) -es decir, m filas y una columna, siendo m el número de neuronas de la capa- y llamamos al resultado b:
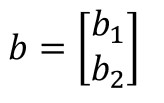
...podemos expresar el vector de salida, y, con la siguiente expresión:
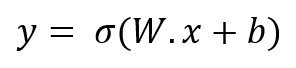
En efecto, si desarrollamos la expresión anterior obtenemos:
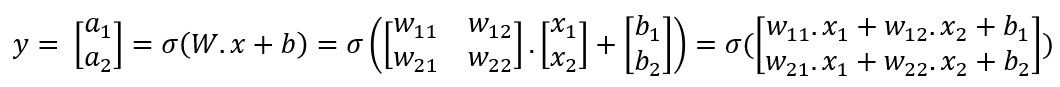
Esta última expresión se puede desarrollar también de la siguiente forma:
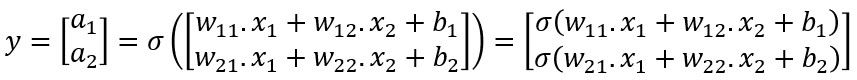
Comprobamos que, efectivamente, el resultado obtenido es exactamente el que habíamos calculado en [1] y [2], pero en forma matricial.