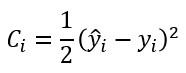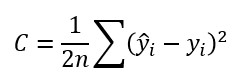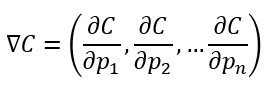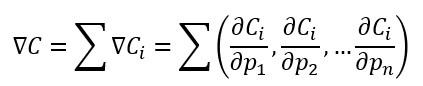Sabemos que, para el cálculo del gradiente de la función de coste debemos pasar las muestras del mini-batch por la red, obtener el error y, a partir de él, el gradiente. Y tal vez te estés preguntando si tiene sentido este enfoque que estamos planteando consistente en inicializar el gradiente total, obtener el gradiente para cada muestra e ir acumulándolo en el gradiente total. La respuesta es sí -al menos para cierto tipo de funciones de coste-. Por ejemplo, supongamos que definimos el error cometido para una única muestra con la siguiente expresión:
(el dividir por 2 hace más sencilla la expresión de su derivada)
Y supongamos que definimos el error para todas las muestras como el valor medio de estos errores parciales:
Esto supone que el gradiente asociado a C...
(siendo pi cada uno de los parámetros de la red) ...puede obtenerse como la suma de los gradientes asociados a cada muestra:
(recordemos lo ya comentado acerca del cálculo de la derivada de una suma de funciones)
Y esto es exactamente lo que estamos planteando: inicializar el gradiente total (pues hay que calcular la derivada parcial para todos los parámetros de la red, es decir, para todos los pesos y bias de cada capa) e ir añadiendo el gradiente correspondiente a cada una de las muestras del mini-batch.