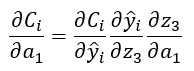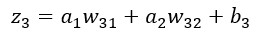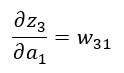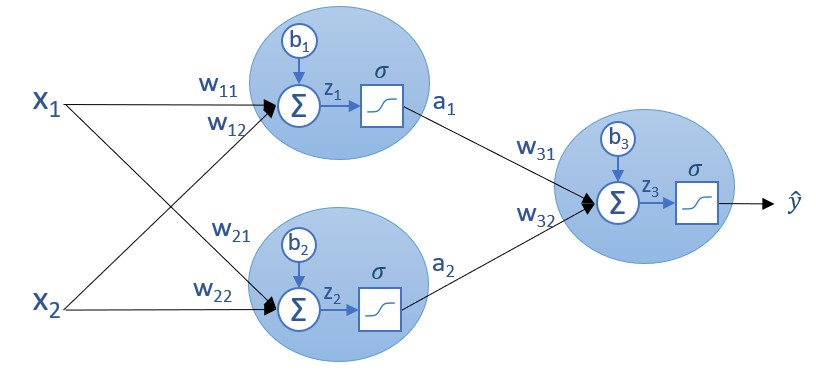
Lo interesante de esto es que, una vez calculadas estas derivadas parciales, podemos usar la regla de la cadena para seguir recorriendo la red neuronal de derecha a izquierda, calculando el resto de derivadas parciales. Así, si quisiéramos calcular la derivada parcial de la función de coste parcial Ci con respecto a a1 podríamos hacerlo aplicando la regla de la cadena:
Si tenemos en cuenta la relación entre a1 y z3:
...podemos calcular la derivada parcial de z3 con respecto a a1:
...y así sucesivamente. Y recordemos que para obtener la función de coste total C bastaría con sumar las funciones de coste parciales.
El resultado de este proceso para una única muestra es el conjunto de derivadas parciales de la función de coste con respecto a cada parámetro achacables a dicha muestra.
Si llamamos a este resultado "gradiente parcial" (achacable a una muestra), la suma de todos los gradientes parciales forma el llamado gradiente o vector gradiente de la función de coste, vector que apunta -tal y como hemos visto- en la dirección de máximo crecimiento de la función (en este caso de la función de error).
Este vector es el gradiente de la función de coste para todas las muestras del dataset con el que estemos entrenando a nuestra red neuronal.
Como podemos ver, es este cálculo iterativo que recorre la red de derecha a izquierda el que da el nombre a este método de aprendizaje: backpropagation o retropropagación en español.