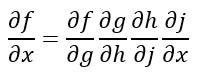La solución a este problema es la llamada regla de la cadena. Ésta nos dice que, si una función f depende de la función g, y que ésta, a su vez, depende de la variable x, podemos expresar la derivada de f con respecto a x de la siguiente manera:
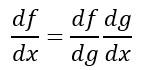
Es decir, la derivada de f con respecto a x puede expresarse como el producto de la derivada de f con respecto a g y la derivada de g con respecto a x. En el caso de estar trabajando con derivadas parciales la regla es la misma:
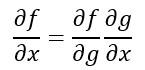
Esta regla se puede aplicar de forma iterativa. Así, si la función f depende de la función g, la función g de la función h, ésta de la función j, y j depende de x, podemos calcular la derivada parcial de f con respecto a x de la siguiente forma: