Esto nos invita a remontarnos en el tiempo hasta 1888, año en el que el científico español Santiago Ramón y Cajal publicó un artículo científico en el que describía las neuronas que había conseguido identificar en el cerebro de ciertas aves. Este descubrimiento llevó a numerosos científicos a estudiar la simulación del comportamiento de dichas neuronas mediante sistemas artificiales.
La primera neurona artificial fue desarrollada en 1943 por el neurólogo y cibernético Warren Sturgis McCulloch y el matemático Walter Harry Pitts: la conocida como “Neurona de McCulloch-Pitts”. Este desarrollo fue mejorado por el psicólogo Frank Rosenblatt en 1958, siendo su neurona conocida como “Perceptrón”:
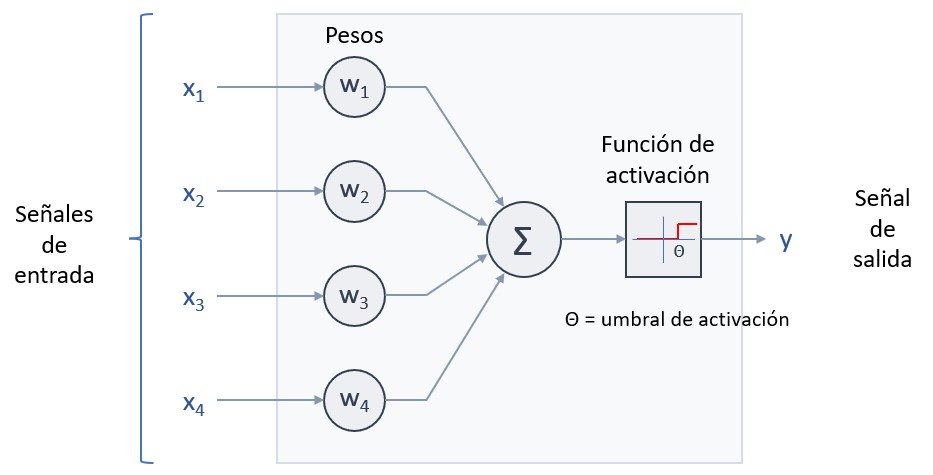
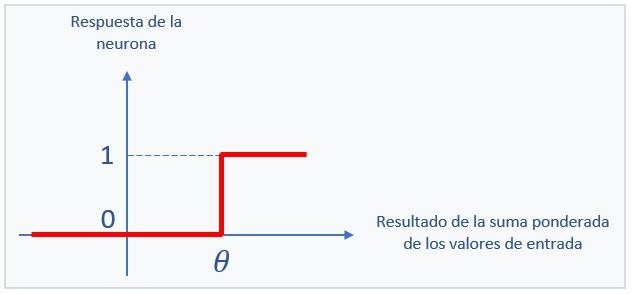
Como vemos en la imagen anterior, al Perceptrón llegaban n señales de entrada x1, x2… xn (es decir, un vector x de n elementos, 4 en el ejemplo mostrado), señales que tenían que ser binarias (solo podían tomar los valores 0 o 1). Cada una de las señales de entrada tenía asociada un peso (w1, w2…wn), pesos que habían sido fijados durante la configuración de la neurona. Cuando llegaba a ella un vector x de entrada, la neurona multiplicaba cada valor xi por su peso asociado wi, sumaba los valores parciales obtenidos y comparaba dicho resultado con un umbral Θ que representaba la sensibilidad de la neurona. Si el resultado era igual o mayor que este umbral, la neurona se activaba y generaba un 1. Por el contrario, si el resultado era inferior al umbral Θ, la neurona no se activaba y generaba un 0.
Esta función que se aplica al resultado del sumatorio recibe el nombre de función de activación y, en el caso de la neurona de Rosenblatt, se trataba de una función escalón: