En el ejemplo anterior hemos planteado una función (una función de error) que dependía de una única variable (de un parámetro del algoritmo), lo que no va a ser lo común, pues, normalmente, el algoritmo involucrará muchos parámetros. En una Adaline con 3 variables de entrada tendremos, por ejemplo, cuatro parámetros: tres pesos (uno para cada una de las variables de entrada) y el bias. De hecho, en las redes neuronales más complejas que se usan hoy en día, el número de parámetros ronda el billón.
Trabajando con funciones que dependen de más de una variable, el concepto de derivada se generaliza en el concepto de gradiente. Al igual que la derivada, el gradiente representa la pendiente de la línea tangente a la función, pero, en este caso, para cada una de sus variables (o parámetros).
Formalmente hablando, podemos decir que el gradiente en un punto se define como un vector formado por las derivadas parciales de la función con respecto a cada una de las variables de la función. Por ejemplo, si la función f depende de a y b, como en nuestro ejemplo, para un punto de la función (es decir, para una combinación dada de a y b), el gradiente estará formado por la derivada de la función con respecto a la variable a y por la derivada de la función con respecto a la variable b, lo que se representa con la siguiente expresión:
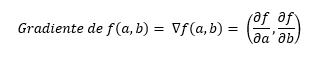
Si tuviésemos una función de 5 variables, el gradiente estaría formado por 5 valores, uno por cada variable.