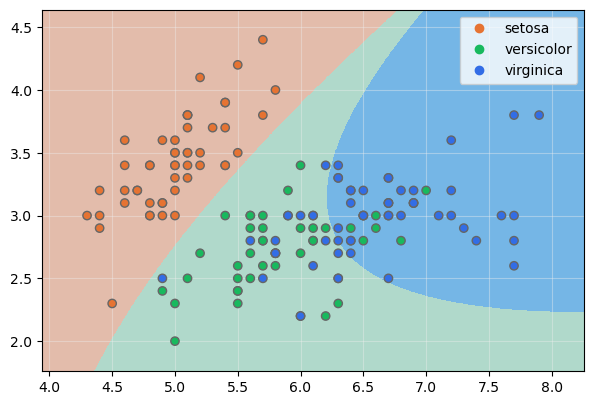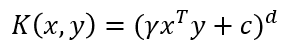
Podemos simular el kernel lineal con el polinómico, especificando grado 1 (aquí sí podríamos especificar la constante c):
model = SVC(kernel = "poly", degree = 1, gamma = 1, coef0 = 0)
model.fit(X.values, y)
show_boundaries(model, X.values, None, y, None, labels = iris.species.unique())
model.fit(X.values, y)
show_boundaries(model, X.values, None, y, None, labels = iris.species.unique())
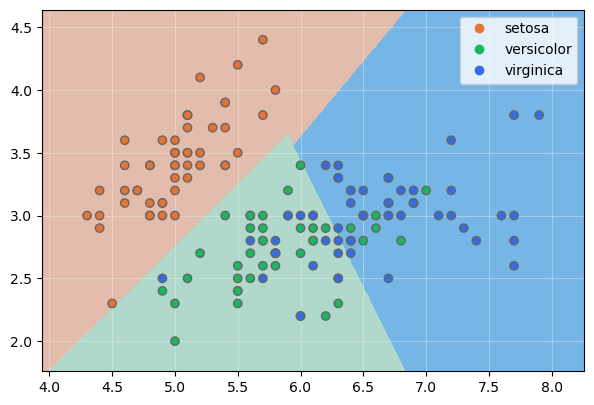
Si especificamos grado 2, estaremos convirtiendo nuestro dataset a un espacio de 4 dimensiones:
model = SVC(kernel = "poly", degree = 2)
model.fit(X.values, y)
show_boundaries(model, X.values, None, y, None, labels = iris.species.unique())
model.fit(X.values, y)
show_boundaries(model, X.values, None, y, None, labels = iris.species.unique())
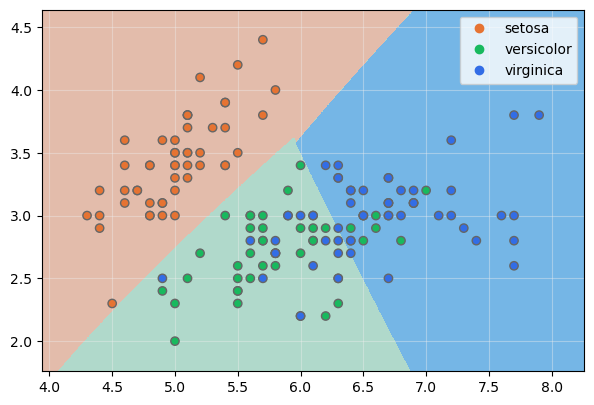
Con grado 3, a un espacio de 6 dimensiones:
model = SVC(kernel = "poly", degree = 3)
model.fit(X.values, y)
show_boundaries(model, X.values, None, y, None, labels = iris.species.unique())
model.fit(X.values, y)
show_boundaries(model, X.values, None, y, None, labels = iris.species.unique())
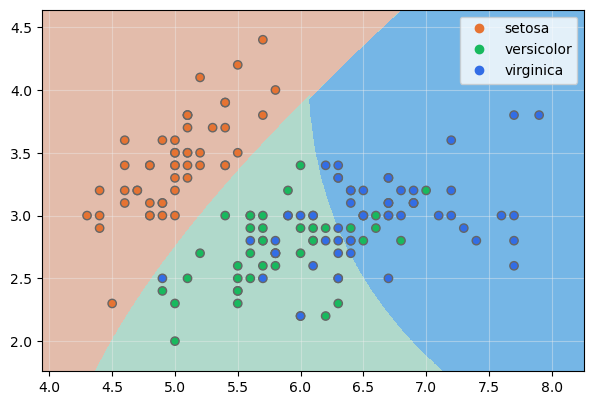
Obsérvese la influencia del coeficiente de regularización (la fuerza de la regularización es inversamente proporcional a C, siendo C = 1 el valor por defecto):
model = SVC(kernel = "poly", degree = 3, C = 10)
model.fit(X.values, y)
show_boundaries(model, X.values, None, y, None, labels = iris.species.unique())
model.fit(X.values, y)
show_boundaries(model, X.values, None, y, None, labels = iris.species.unique())