En funciones que dependen de una única variable, como f(x), la derivada de f(x) en un punto determina la rapidez con la que la función cambia en dicho punto. Si la derivada en un punto es cero, significa que la función en dicho punto es horizontal (ni sube ni baja). Si la derivada en un punto es un número positivo (como... 8), significa que la función crece en ese punto. Por último, si la derivada en un punto es un número negativo (como... -8), significa que la función decrece en ese punto. El concepto de derivada en un punto se muestra gráficamente dibujando la recta tangente a la función en dicho punto. Veamos un ejemplo:
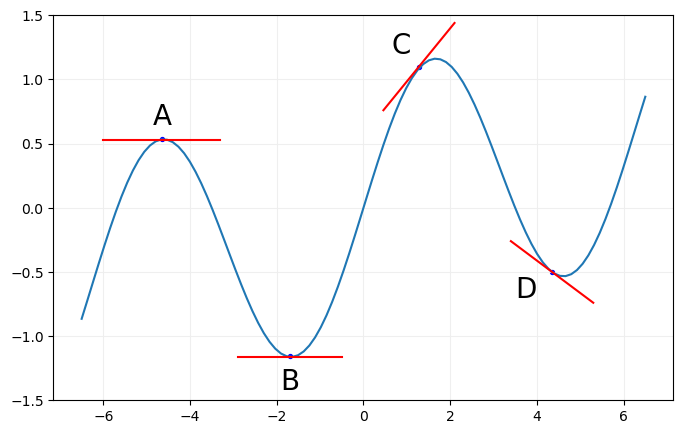
En la función mostrada en la imagen anterior se han escogido 4 puntos, A, B, C y D y se han dibujado (en rojo) las rectas tangentes a la función en dichos puntos: En A y en B la tangente es una línea horizontal, lo que significa que la función, en dichos puntos, es horizontal y su derivada en ellos es cero. La tangente en el punto C es una línea creciente, lo que significa que la derivada de la función en C es un número positivo (por ejemplo... 2). En D la tangente es decreciente, lo que implica que la derivada es negativa, tal vez... -1.