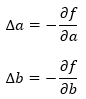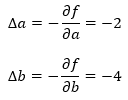Para ver de qué nos sirve esto, pongamos un caso concreto. Imaginemos que, en nuestro ejemplo de la recta de regresión ax + b, estamos evaluando el punto (10, 5) (es decir, supongamos que estamos considerando la combinación a = 10 y b = 5 como posibles parámetros “óptimos”), y sigamos suponiendo que el error cometido para cada pareja de valores a y b viene dado por la siguiente superficie:
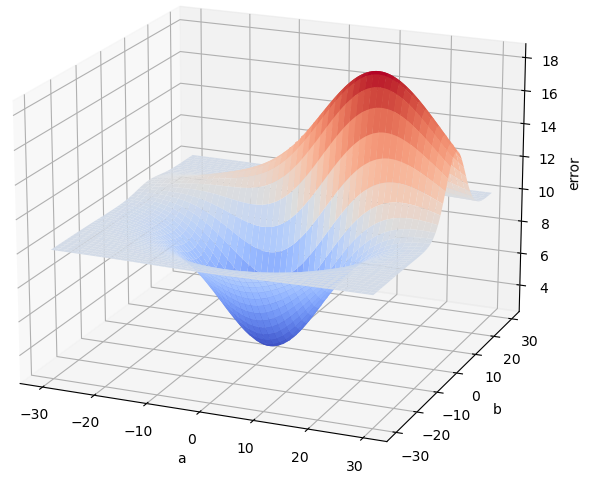
Supongamos ahora que, en dicho punto, el error es, por ejemplo, 50 (los valores no son relevantes, solo es un ejemplo). Calculamos el gradiente de la función de error con respecto a las variables a y b en el punto (10, 5) y obtenemos el vector (2, 4). El "2" significa que, si el parámetro a aumenta, la función (el error en nuestro caso) aumenta. De hecho, el "2" significa que si a aumenta en una cierta cantidad (tiene que ser pequeña para que esto sea cierto), el error aumenta el doble. El "4" implica algo parecido: Si b aumenta en una cierta cantidad, el error aumenta la misma cantidad multiplicada por 4.
Pero esto también podría interpretarse diciendo que, si a disminuye un poco, el error disminuiría el doble de la cantidad que restemos a dicho parámetro. Y que, si b disminuye un poco, el error disminuiría cuatro veces la cantidad que restemos a este parámetro. Y recordemos que nuestro objetivo es disminuir el error, de forma que la estrategia está clara: tenemos que restar a nuestros parámetros una cierta cantidad para disminuir el error. ¿Qué cantidad? Una opción es considerar como valor a restar la derivada parcial de la función de error con respecto al parámetro de que se trate. De esta forma, si la derivada parcial es alta (4, por ejemplo) significaría que la recta tangente está muy inclinada, que, por lo tanto, estamos lejos del valor mínimo y que podemos restar a nuestro parámetro una cantidad mayor. Si, por el contrario, la derivada parcial fuese pequeña (0.01, por ejemplo), significaría que la recta tangente es casi horizontal, que, en consecuencia, estamos cerca del valor mínimo, y que conviene restar a nuestro parámetro una pequeña cantidad para no sobrepasar el mínimo que estamos buscando. Es decir, si con el símbolo Δ entendemos “incremento”, una primera idea sería restar a nuestros parámetros la derivada parcial de la función de error con respecto a cada parámetro:
Y es que, en el ejemplo puesto, las dos derivadas parciales (4 y 2) eran positivas. Pero con las fórmulas anteriores estamos cubriendo también la posibilidad de que sean negativas. Por ejemplo, si una de las derivadas parciales es negativa (-2, por ejemplo), significaría que la recta tangente a la función disminuye, lo que supone que, si aumentamos un poco el valor del parámetro, nos acercaremos un poco al mínimo de la función. Al considerar como incremento el valor negativo de la derivada parcial estaríamos añadiendo un incremento positivo a nuestro parámetro, pues –(–2) = +2.
En nuestro ejemplo habíamos presupuesto que las derivadas parciales de la función de error con respecto a los parámetros a y b eran 4 y 2 respectivamente, de forma que los incrementos a aplicar serían:
Es decir, si restamos a cada parámetro el valor de la derivada parcial correspondiente, estamos acercándonos al mínimo de la función más rápidamente cuanto mayor sea la derivada parcial (cuanto más lejos estemos del mínimo que buscamos) y más lentamente cuanto menor sea la derivada parcial (cuanto más cerca estemos del mínimo que estamos buscando).