A continuación, vamos a modificar la escala de los datos para evitar que el Perceptrón requiera aplicar incrementos demasiado grandes a los pesos, mejorando, por tanto, el rendimiento del entrenamiento.
Aunque se hablará más delante de los métodos de escalado ofrecidos por Scikit-learn, en esta primera ocasión vamos a utilizar una clase -la clase StandardScaler- que elimina el valor medio de los datos y los escala de forma que su desviación estándar sea 1.
Echemos un vistazo previo a, por ejemplo, los valores de la primera característica predictiva contenida en nuestro dataset de entrenamiento, X_train:
plt.show()
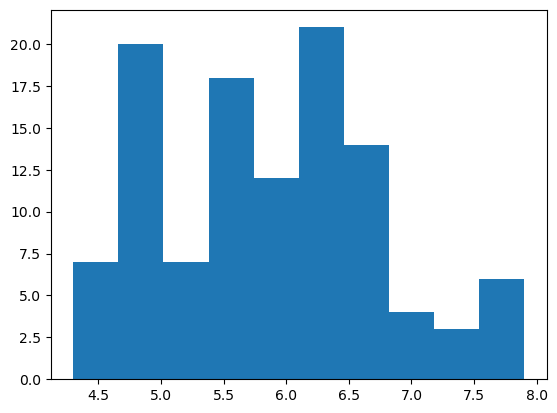
Vemos que los valores se distribuyen en un rango aproximado de 4 a 7 cm.
Importemos e instanciemos la clase StandardScaler:
Ahora debemos entrenar el escalador y aplicarlo a los datos:
X_test_std = scaler.transform(X_test)
El método .fit_transform() entrena el escalador a partir de los datos que se le pasen como argumento, y transforma éstos devolviendo un array NumPy con los datos transformados. El método .transform() simplemente aplica el escalador ya entrenado a otros datos, devolviéndolos en un array NumPy.
Obsérvese que, para el entrenamiento del escalador, estamos basándonos apenas en el bloque de entrenamiento X_train. De esta forma nos aseguramos de que el modelo a generar solo se basa en datos conocidos.
Los valores de la primera característica predictiva del bloque de entrenamiento tienen ahora la siguiente distribución:
plt.show()
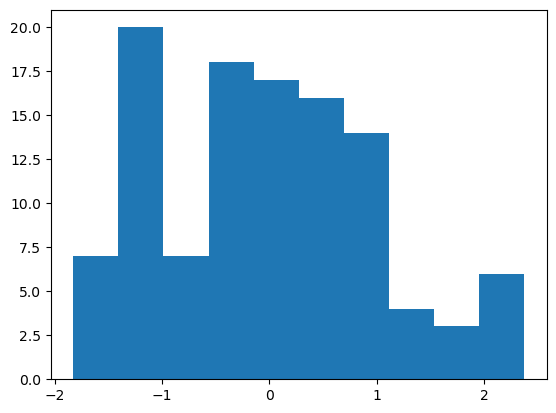
(recordemos que, ahora, las estructuras X_train_std e X_test_std contienen arrays NumPy, no DataFrames Pandas).
Vemos como, tras la transformación, los datos se distribuyen en torno al valor cero, aunque, debido al limitado número de valores contenidos en este array, el aspecto que ofrece no es exactamente el de una distribución gaussiana.