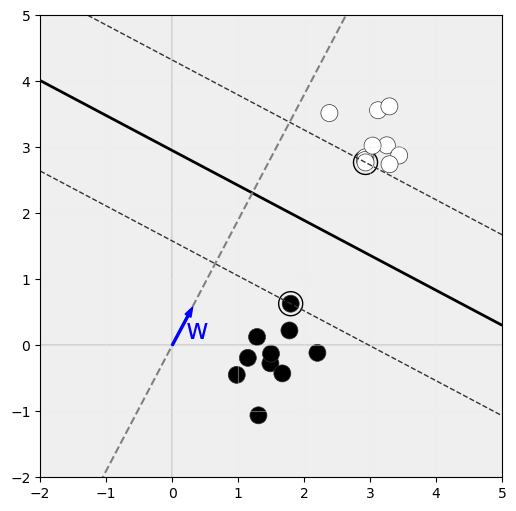
Para este cálculo, vamos a definir un vector w, de longitud indefinida por ahora, que suponemos ortogonal al hiperplano:
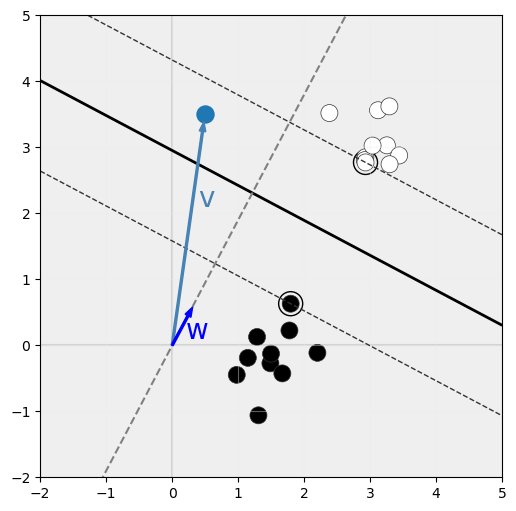
Ahora, dado un punto cualquiera definido por un vector v:
podemos averiguar si recibe una clase u otra proyectándolo sobre la recta definida por w:
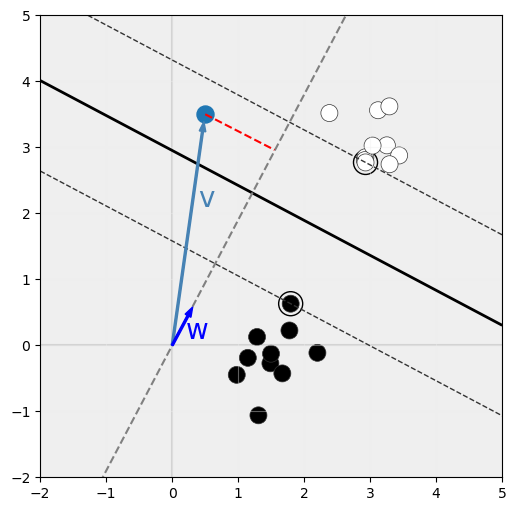
Si el punto definido por el vector v cae más allá del punto de cruce entre la recta definida por w y el hiperplano, recibirá una clase (que supongamos que se trata de la clase positiva). Y si cae antes del punto de cruce, recibirá la clase que supondremos negativa.
Esta proyección del vector v sobre la recta definida por w no es más que el producto escalar de w y v.
De este modo, podemos fijar -para el vector w que todavía estamos buscando- una "constricción" para cada punto de nuestro dataset: los de la clase positiva deberán caer más allá del hiperplano, y los de la clase negativa deberán caer más cerca.