Para ver de qué nos sirve esto, pongamos un caso concreto. Imaginemos que, en nuestro ejemplo de la red neuronal que depende de dos únicos parámetros (a y b) estamos en el punto (10, 5) (es decir, supongamos que a toma el valor 10 y b toma el valor 5).
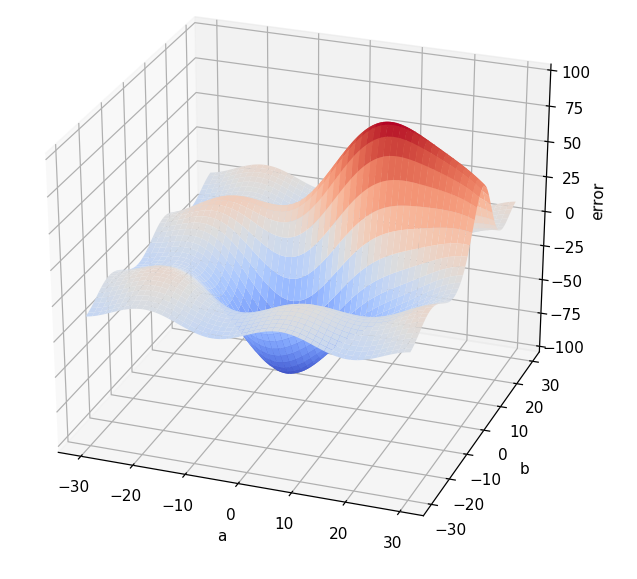
En dicho punto el error es, por ejemplo, 50 (los valores nos dan igual, solo es un ejemplo). Calculamos el gradiente de la función de error con respecto a las variables a y b en el punto (10, 5) y obtenemos el vector (2, 4). El "2" significa que si a aumenta, la función (el error en nuestro caso) aumenta. De hecho, el "2" significa que, si a aumenta en una cierta cantidad (tiene que ser pequeña para que esto sea cierto), el error aumenta el doble. El "4" implica algo parecido: Si b aumenta en una cierta cantidad, el error aumenta la misma cantidad multiplicada por 4.
Entonces, si al aumentar a y b aumenta el error, si disminuimos a y b ¡el error deberá disminuir! Si por Δ entendemos "incremento", los incrementos a aplicar a a y a b para disminuir el error podrían ser los siguientes:
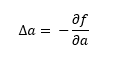
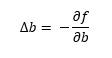
En otras palabras: si la derivada parcial de la función con respecto a la variable a es positiva, significa que al aumentar a aumenta el valor devuelto por la función, así que si restamos algo a a disminuiremos el valor devuelto por la función. Así que restemos a a su derivada parcial: si dicha derivada parcial es muy alta, significa que el error aumenta muy rápidamente al aumentar a, de forma que podemos restar a a una cantidad "alta" para ir "en la dirección contraria" (en la dirección en la que la función decrece). Si la derivada parcial fuese pequeña, significaría que al aumentar a, la función aumenta "un poco", de forma que no queremos quitar a a un valor demasiado grande. Al restar la derivada parcial, estamos quitando más cuando la función crece más, y quitamos menos cuando la función crece menos.