La matriz de pesos contiene los pesos de los enlaces que llegan a la capa de la red neuronal que estemos considerando. En el ejemplo que hemos visto la única capa oculta contiene dos neuronas a la que llegan enlaces de las dos neuronas de la capa de entrada:
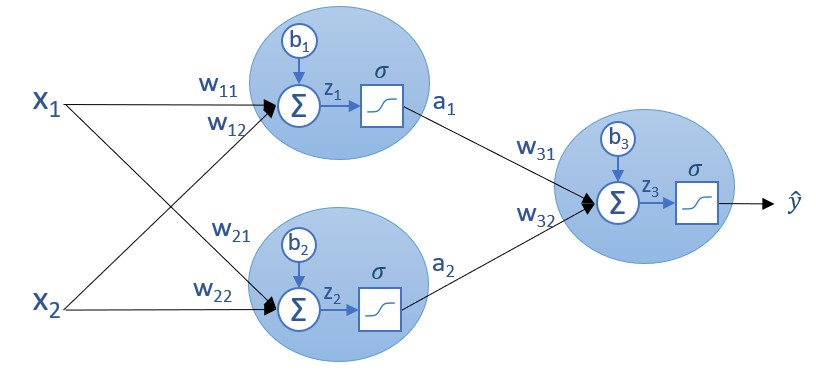
Los cuatro pesos involucrados son los que hemos llamado w11, w12, w21 y w22. Pues bien, la matriz de pesos a la que hemos llamado W tendrá tantas filas como neuronas tenga la capa a la que llegan los enlaces (dos en este ejemplo) y tantas columnas como valores lleguen a la capa (dos también en este ejemplo). En la matriz W, el elemento wij (el elemento que ocupa la fila i y la columna j) es el peso del enlace que llega a la neurona i-ésima desde la neurona j-ésima de la capa anterior:
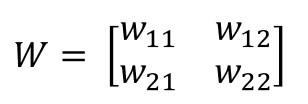
En un caso más general la matriz se expresaría de la siguiente forma:
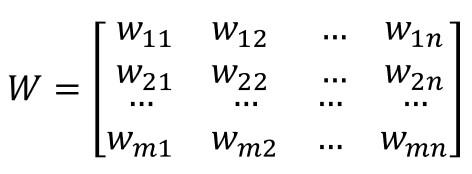
...expresión en la que m es el número de neuronas de la capa y n es el número de neuronas de la capa anterior.