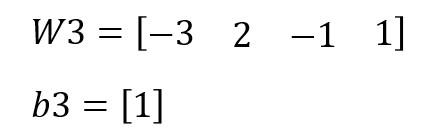Ahora que sabemos cómo obtener la salida de una capa a partir de las matrices formadas por los valores de entrada, los pesos y los bias, podríamos plantearnos la forma de aplicar este método a una red neuronal formada por más de una capa.
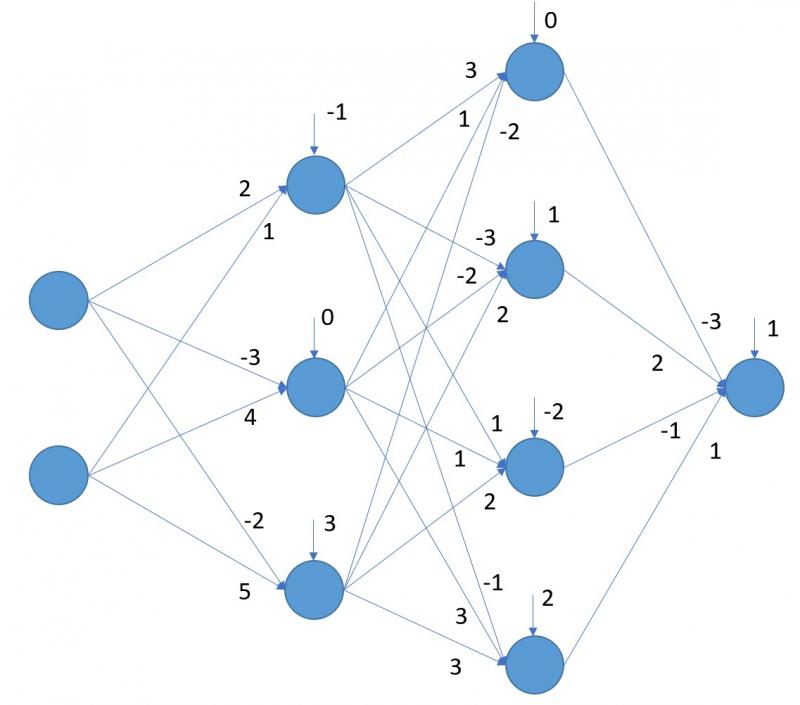
Consideremos, por ejemplo, la siguiente red en la que se ha indicado el valor de los pesos y bias de todas las capas (menos de la capa de entrada, obviamente):
Obtengamos las matrices de cada una de las capas. Para la primera capa tendríamos la siguiente matriz de pesos (a la que vamos a llamar W1):
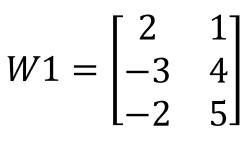
...y la siguiente matriz de bias (a la que llamamos b1):
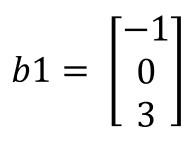
Para la segunda capa, las matrices (W2 y b2) serían las siguientes:
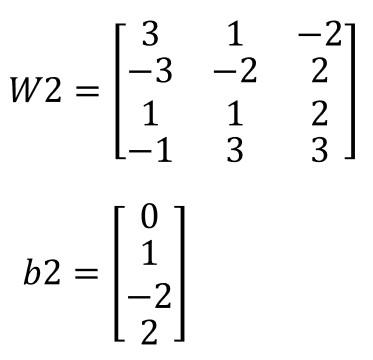
Y para la tercera capa, serían: