Supongamos ahora que la entrada a la red son los valores 3 y 1, valores que, como ya sabemos, deberemos representar por medio de una matriz formada por dos filas y una única columna:
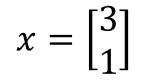
Ahora podríamos calcular la salida de la primera capa oculta (valores y1, y2 e y3 de la siguiente imagen) realizando el cálculo ya conocido:
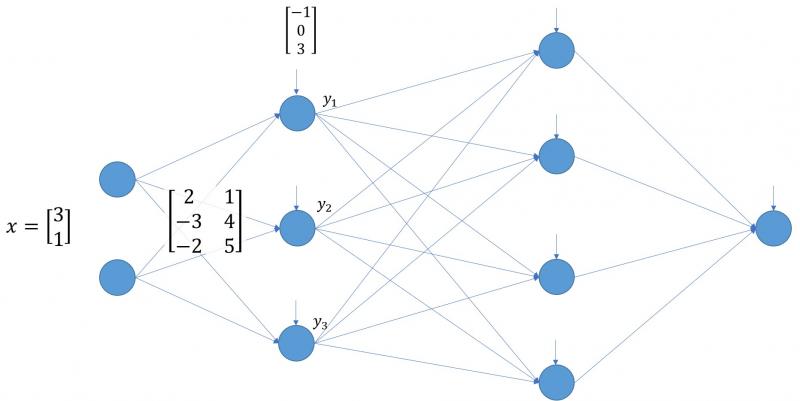
Si llamamos y al vector formado por y1, y2 e y3, tenemos que:
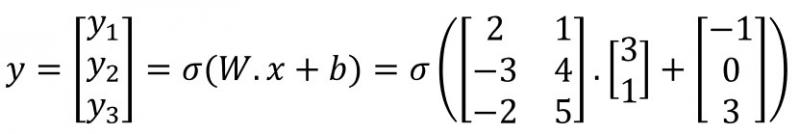
Realicemos el cálculo usando Python considerando como variables W1 (matriz de pesos), b1 (matriz de bias) y x1 (matriz de valores de entrada):
La matriz de pesos vendría dada por:
W1 = np.array([2, 1, -3, 4, -2, 5]).reshape(3, -1)
W1
array([[ 2, 1],
[-3, 4],
[-2, 5]])
...la matriz de bias por:
b1 = np.array([-1, 0, 3]).reshape(3, 1)
b1
array([[-1],
[ 0],
[ 3]])
...y la matriz de entrada sería la siguiente:
x1 = np.array([3, 1]).reshape(2, 1)
x1
array([[3],
[1]])
Por lo tanto:
y = sigmoid(W1.dot(x1) + b1)
y
array([[0.99752738],
[0.00669285],
[0.88079708]])
Es decir, la salida de la neurona superior de la primera capa oculta es 0.99752738, la de la neurona intermedia es 0.00669285, y la de la neurona inferior es 0.88079708:
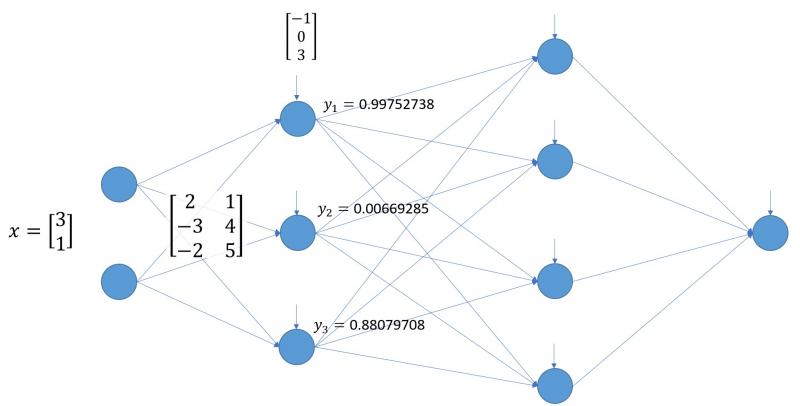
Lógicamente, estos valores de salida de la primera capa oculta serán los valores que alimenten la siguiente capa.