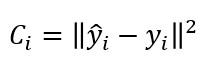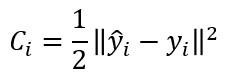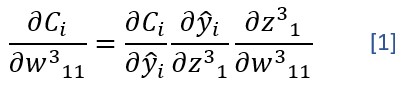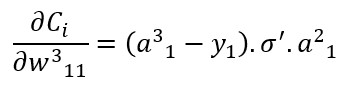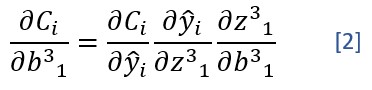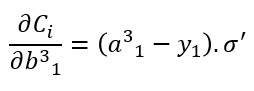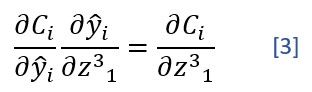Ya hemos planteado el tipo de función de coste que sería necesaria para un entorno de clasificación como el nuestro, por ejemplo -para una muestra-:
En todo caso, en nuestra implementación vamos a aplicar esta misma función de coste con un pequeño retoque:
Esto nos va a permitir "librarnos" de los doses cuando calculemos la derivada de esta función con respecto a ȳi.
Si repitiésemos ahora el cálculo de la derivada parcial de la función de coste con respecto a un peso -el w311, por ejemplo- obtendríamos:
Es decir:
Y el cálculo de la derivada parcial con respecto al bias b31 -por ejemplo- sería:
Es decir:
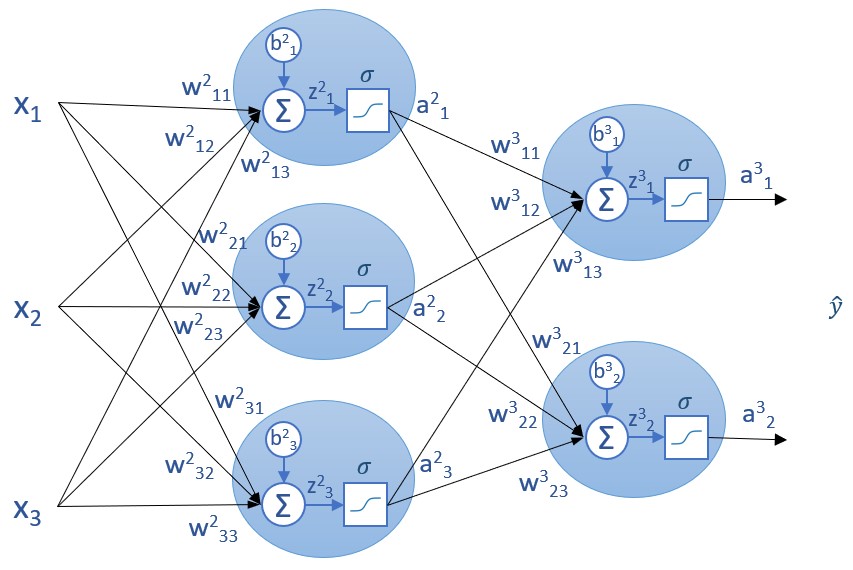
(recordemos que, en nuestra red, los valores ai de la última capa coinciden con lo que estamos llamando yi -la predicción- para cada clase).
En las expresiones anteriores, y1 es el valor de la variable objetivo, y, para la primera neurona.
Obsérvese que expresiones [1] y [2] tienen un factor común, correspondiente a la derivada parcial de la función de coste con respecto a z:
Y es precisamente esta derivada parcial la que nos va a permitir "saltar" a la capa anterior: Como veremos en la siguiente sección, la derivada parcial de la función de coste con respecto a un parámetro de la capa n la vamos a calcular haciendo referencia a la derivada parcial de la función de coste con respecto al valor z de la capa n+1.
El cálculo de la derivada parcial definida en la expresión [3] para la capa de salida de la red nos devuelve (ŷi - yi).σ', valor que podemos calcular y guardar en una variable a la que vamos a llevar delta:
delta = (a_layers[-1] - y) * sigmoid_derivative(z_layers[-1])
...variable a la que haremos referencia cuando nos movamos a la siguiente capa.
Aquí, a_layers[-1] son los valores devueltos por las funciones de activación de la última capa (es decir, las predicciones), y z_layers[-1] son los valores z a los que se aplica la función sigmoide.
Debemos tener en cuenta que a_layers[-1] es un array conteniendo los valores "a" de todas las neuronas de la capa de salida, y lo mismo puede decirse de z_layers[-1]. Esto significa que delta contiene un array con tantos valores como neuronas hay en la capa de salida.
Ahora, el cálculo de la derivada de la función de coste con respecto a los bias es exactamente delta.
grad_b[-1] = delta
(y, nuevamente, en este gradiente hay un valor para cada neurona de la capa de salida)
...y el cálculo de la derivada de la función de coste con respecto a los pesos es igual al producto escalar de delta por los valores devueltos por la capa anterior: a_layers[-2].
grad_w[-1] = np.dot(delta, a_layers[-2].transpose())
(y, también aquí, estamos obteniendo un array con un valor por neurona de la capa de salida).
La transposición de a_layers[-2] es necesaria para poder realizar el producto de ambas matrices.