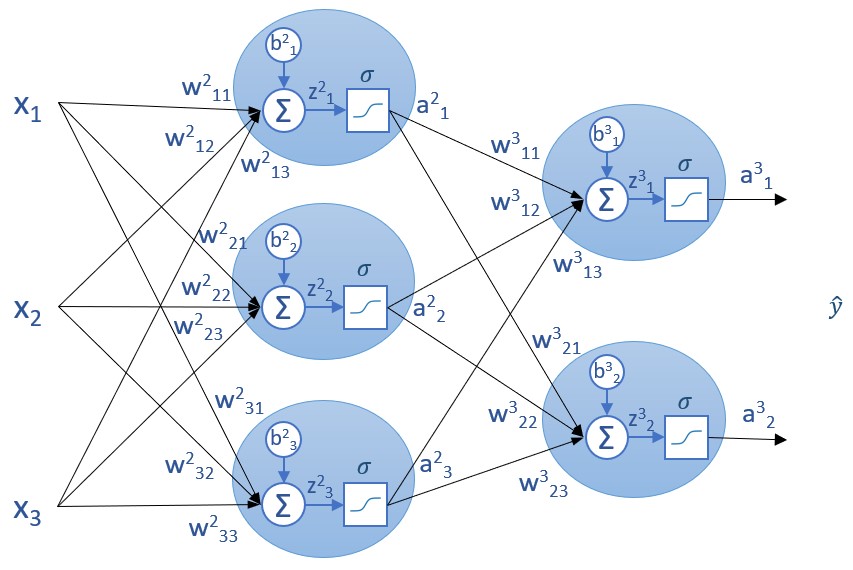
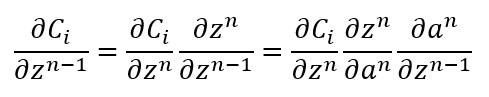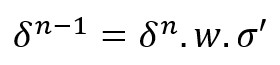Para calcular la derivada parcial de la función de coste con respecto a los parámetros de las capas ocultas no tenemos más que "jugar" con las derivadas parciales y la regla de la cadena. Para empezar, obtengamos la relación entre del "delta" de una capa n-1 (δn-1) y el "delta" de la capa n (δn), siendo "delta" la derivada parcial de la función de coste con respecto a los valores z de una capa:
Recordemos que las capas se numeran de izquierda a derecha, lo que significa que la capa n queda a la derecha de la capa n-1.
La derivada de z con respecto al valor a es igual al peso del enlace del que se trate, y la derivada de a con respecto a z es igual a la derivada de la función de activación. Es decir:
Y una vez obtenido el valor de delta para la capa n-1, podemos calcular las derivadas parciales de la función de coste con respecto a un bias o a un peso de dicha capa tal y como hemos hecho para la capa de salida. Concretamente, para una capa dada consideramos los valores z de la capa anterior:
z = z_layers[-layer]
...y el resultado de la aplicación de la derivada de la función de activación a dichos valores:
sp = sigmoid_derivative(z)
Calculamos el producto de las matrices de pesos y de la matriz delta de la iteración anterior, y multiplicamos el resultado por la derivada sp calculada:
delta = np.dot(self.weights[-layer + 1].transpose(), delta) * sp
La derivada parcial de la función de coste con respecto a los bias coincide con "delta", y la derivada parcial con respecto a los pesos coincide con el producto de "delta" y los valores "a", tal y como hemos visto:
grad_b[-layer] = delta
grad_w[-layer] = np.dot(delta, a_layers[-layer - 1].transpose())
Este cálculo tendremos que realizarlo para todas las capas ocultas quedando, por tanto, el código de la siguiente forma:
for layer in range(2, self.num_layers):
z = z_layers[-layer]
sp = sigmoid_derivative(z)
delta = np.dot(self.weights[-layer + 1].transpose(), delta) * sp
grad_b[-layer] = delta
grad_w[-layer] = np.dot(delta, a_layers[-layer - 1].transpose())